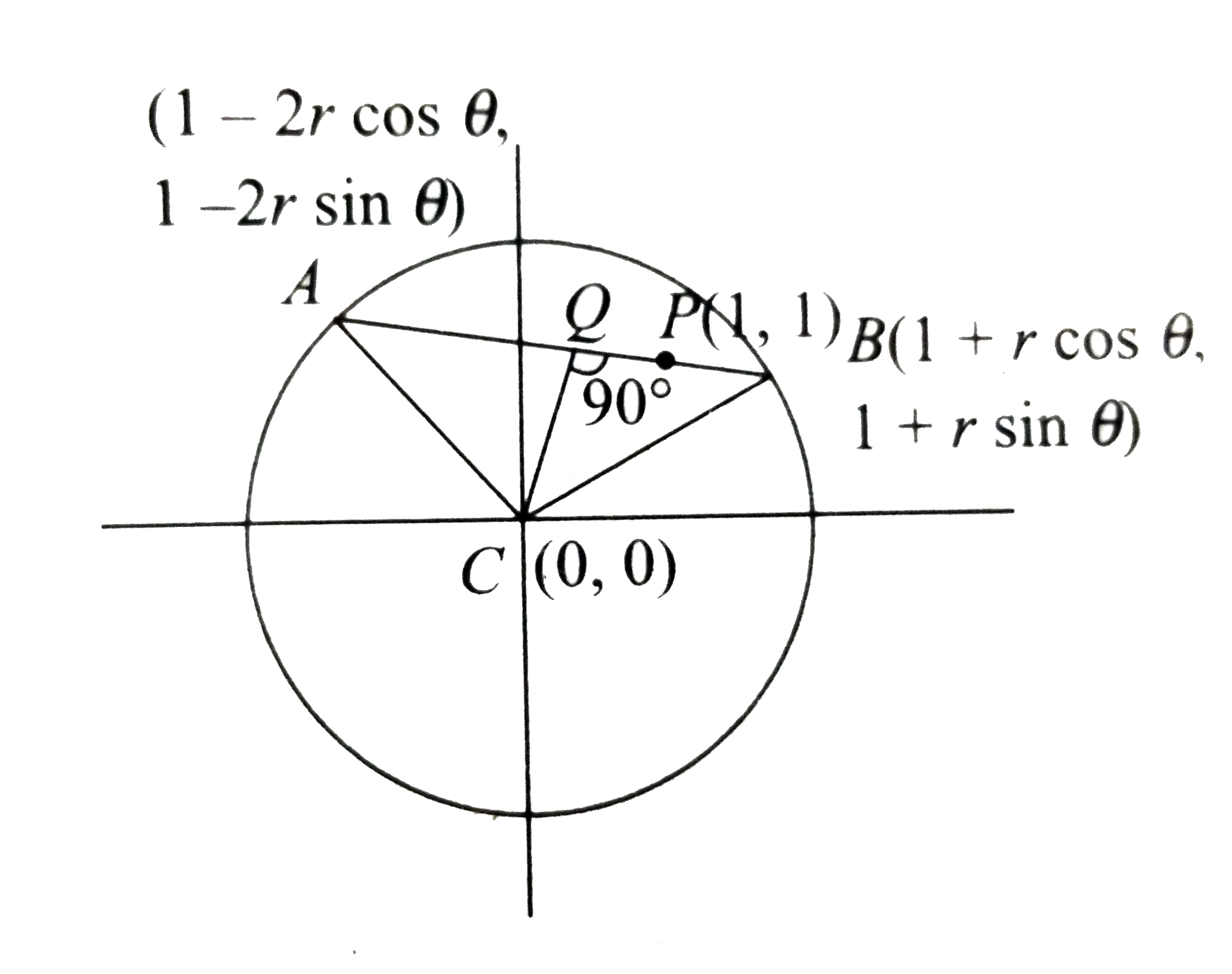A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-CIRCLES-Comprehension Type
- AB is a chord of x^2 + y^2 = 4 and P(1, 1) trisects AB. Then the leng...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- In the diagram as shown, a circle is drawn with centre C(1,1) and radi...
Text Solution
|
- Let P(alpha,beta) be a point in the first quadrant. Circles are drawn ...
Text Solution
|
- P(α,β) is a point in first quadrant. If two circles which passes throu...
Text Solution
|
- Let P(alpha,beta) be a point in the first quadrant. Circles are drawn ...
Text Solution
|
- P(a,5a) and Q(4a,a) are two points. Two circles are drawn through thes...
Text Solution
|
- Two circles are drawn through the points (a,5a) and (4a, a) to touch t...
Text Solution
|