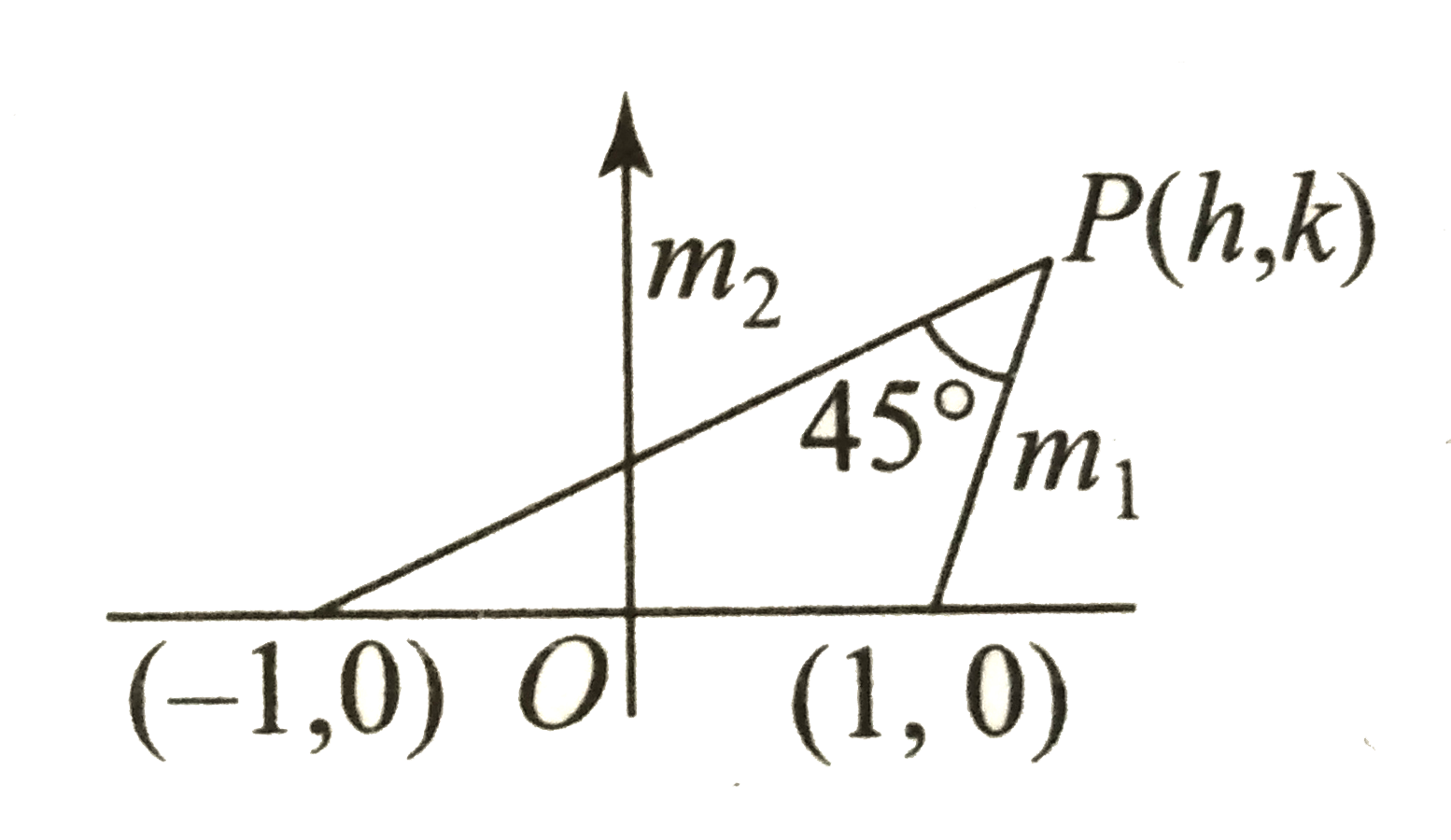
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE PUBLICATION-CIRCLES-Multiple Correct Answers Type
- The line 3x+6y=k intersects the curve 2x^2+3y^2=1 at points A and B . ...
Text Solution
|
- Consider the circle x^2+y^2 -8x-18y +93=0 with the center C and a poi...
Text Solution
|
- Consider two circles C1: x^2+y^2-1=0 and C2: x^2+y^2-2=0. Let A(1,0)...
Text Solution
|
- The real numbers a and b are distinct. Consider the circles omega(1)...
Text Solution
|
- Consider two circles S, =x^2+y^2 +8x=0 and S2=x^2+y^2-2x=0. Let DeltaP...
Text Solution
|
- A variable circle which always touches the line x+y-2=0 at (1, 1) cuts...
Text Solution
|
- A circle S= 0 passes through the common points of family of circles x^...
Text Solution
|
- Q is any point on the circle x^(2) +y^(2) = 9. QN is perpendicular fro...
Text Solution
|
- Locus of the intersection of the two straight lines passing through (1...
Text Solution
|