Two vertices of an equilateral triangle are `(-1,0)` and (1, 0), and its third vertex lies above the y-axis. The equation of its circumcircle is ____________

Explanation

We have equilateral triangle ABC.

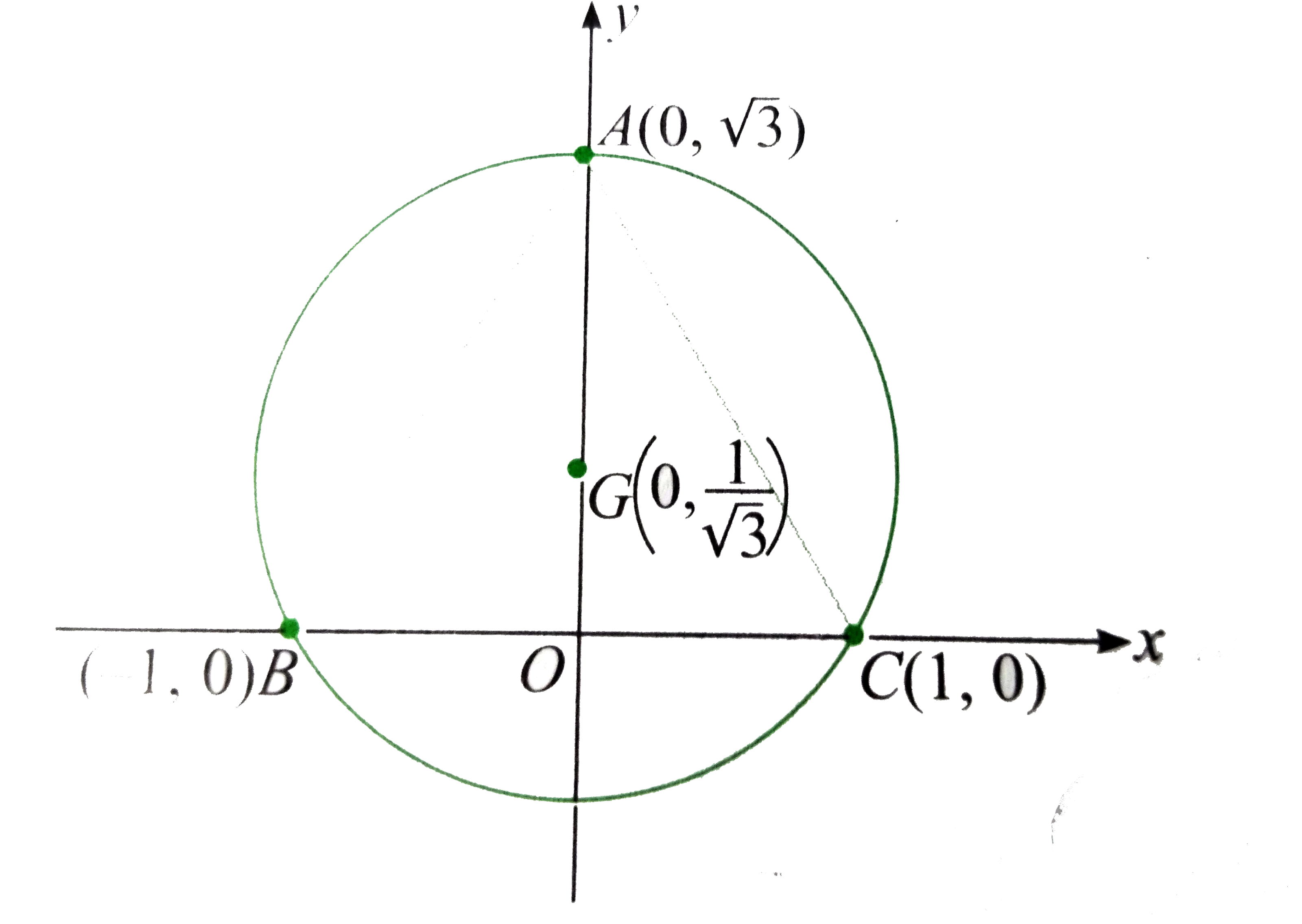
Let `B-= (-1,0), C -= (1,0)`.
Then A lies on y-axis.
`:. OA=AB sin 60^(@)=sqrt(3) `
`:. A -=(0,sqrt(3))`
In an equilateral triangle, circumcentre coincides with centroid.
Thus, circumcentre of triangle ABC is `G-= ((-1+1+0)/(3),(sqrt(3)+0+0)/(3))-=(0,(1)/(sqrt(3)))`
Circumradius `=AG=sqrt(3)-(1)/(sqrt(3))=(2)/(sqrt(3))`
Therefore, equation of circumcircle of triangle ABC is `(x-0)^(2)+(y+(1)/(sqrt(3)))^(2)=((2)/(sqrt(3)))^(2)`