Home
Class 12
MATHS
Find the locus of the midpoint of the ch...

Find the locus of the midpoint of the chords of the circle `x^2+y^2=a^2` which subtend a right angle at the point `(c ,0)dot`

Text Solution

Verified by Experts

Let P(h,k) be the midpoint of a chord AB of the circle which subtends a right angle at C(c,0).

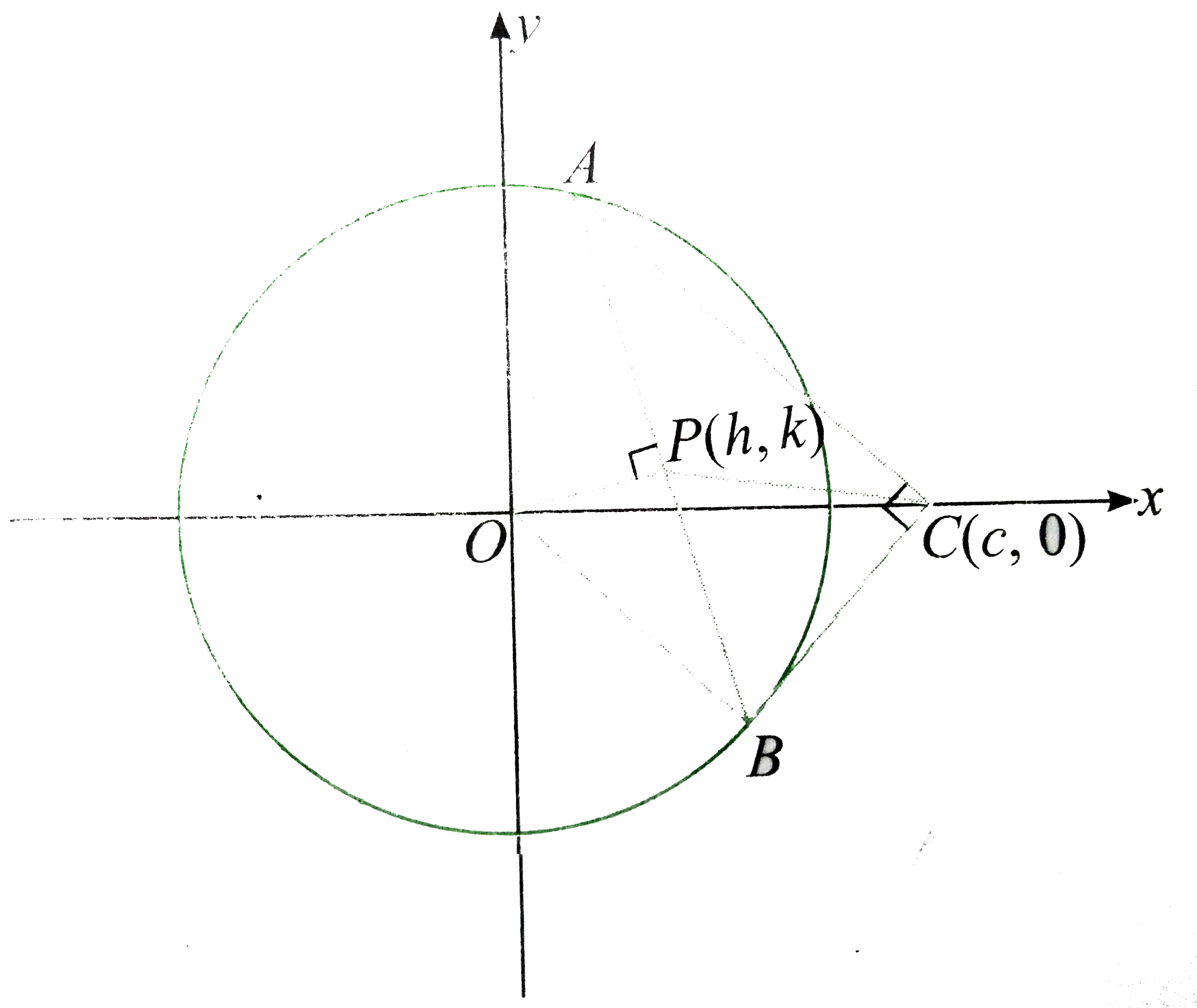
In right angles triangle ACB, we have
`PA=PC=PB`
`PC=sqrt((h-c)^(2)+k^(2))`
`PB=PA=sqrt(OA^(2)-OP^(2))`
`=sqrt(a^(2)-(h^(2)+k^(2)))`
Now , `PC=PA`
`:. sqrt((h-c)^(2)+k^(2))=sqrt(a^(2)-(h^(2)+k^(2)))`
`implies (h-c)^(2)+k^(2)=a^(2)-(h^(2)+k^(2))`
Therefore , the equation of required locus is `2(x^(2)+y^(2))-2cx+c^(2)-a^(2)=0`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Find the locus of the mid point of the chord of the circle x^2+y^2=a^2 which subtend a right angle at the point (0,0).

Find the locus of the midpoint of the chords of the circle x^2+y^2-ax-by=0 which subtend a right angle at the point (a/2 ,b/2)dot is

Find the locus of the midpoint of the chords of the parabola y^2=4ax .which subtend a right angle at the vertex.

The locus of the midpoints of chords of the circle x^(2) + y^(2) = 1 which subtends a right angle at the origin is

Find the locus of mid points of chords of the cirlce. x^(2)+y^(2)=a^(2) which subtend angle 90^(@) at the point (c,o).

Find the locus of the middle points of the chords of the parabola y^2=4a x which subtend a right angle at the vertex of the parabola.

The locus of the midpoint of a chord of the circle x^2+y^2=4 which subtends a right angle at the origins is (a) x+y=2 (b) x^2+y^2=1 x^2+y^2=2 (d) x+y=1

Find the locus of middle points of chords of the ellipse x^2/a^2+y^2/b^2=1 which subtend right angles at its centre.

Find the locus of the midpoint of the chord of the circle x^2+y^2-2x-2y=0 , which makes an angle of 120^0 at the center.

Find the locus of mid points of chords of the cirlce. x^(2)+y^(2)=a^(2) which subtend angle 90^(@) at the centre of the circle.