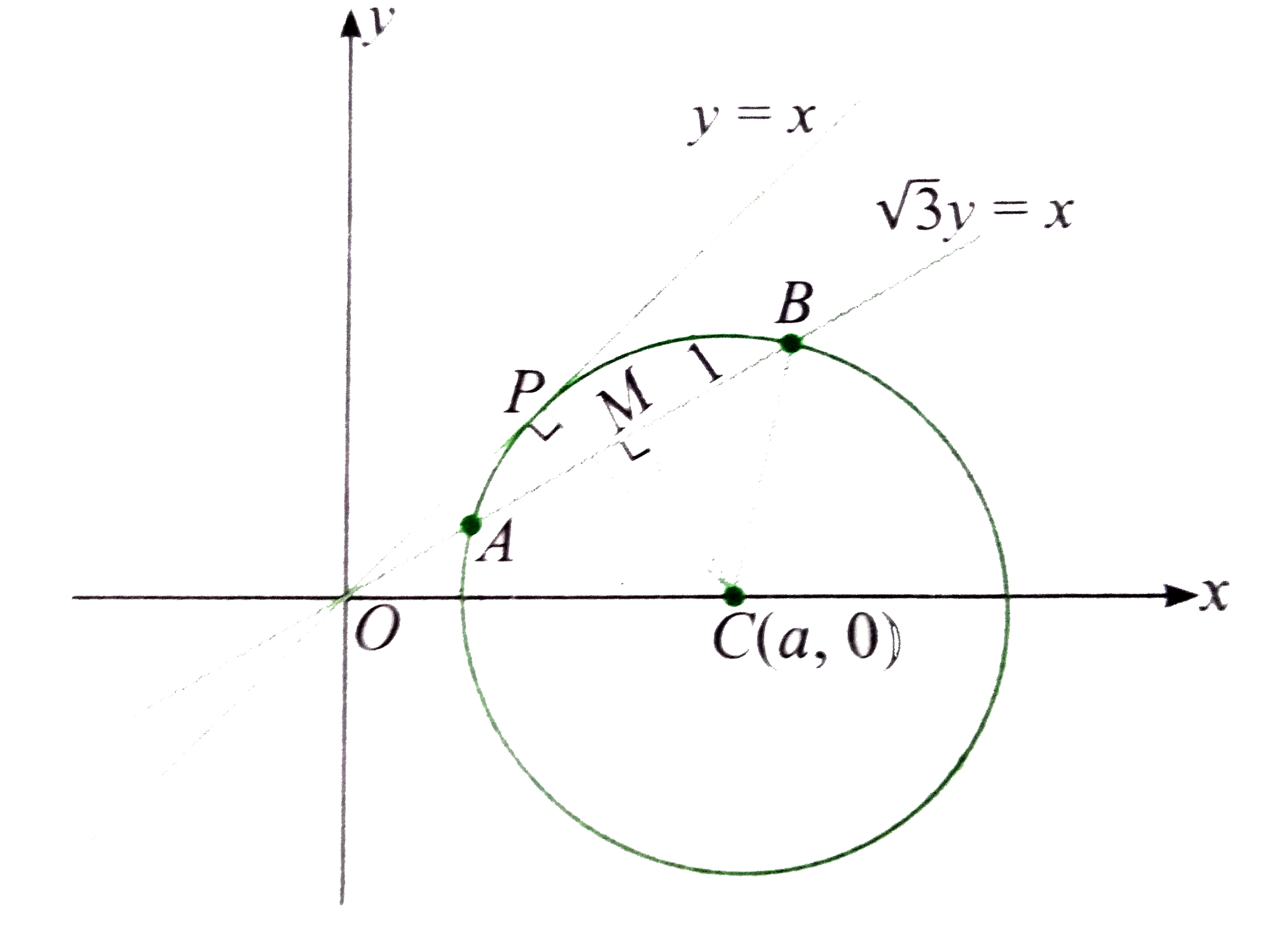
Centre C lies on x-axis.
`:. C-= (a,0)`
Line `y=x` touches the circle at point P.
So, radius of circle is the length of perpendicular (CP) from the centre C on the line `y=x`.
Also, length of chord (AB) of circle on line `x-sqrt(3)y=0` is 2 units.
`:. MB=1(` where m is the midpoint of AB).
Now, `CP=CB" "`(radii of circle)
`:. CP^(2)=CB^(2)`
`implies CP^(2)=CM^(2)+MB^(2)`
`implies ((|a-0|)/(sqrt1^(2)+(-1)^(2)))^(2)=((|a-sqrt(3)(0)|)/(sqrt((3)^(2)+(1)^(2))))^(2)+1^(2)`
`implies (a^(2))/(2)=(a^(2))/(4)+1`
`implies (a^(2))/(4)=1`
`implies a=2` ( as centre lies in first quadrant)
Also, radius `CP=(a)/(sqrt(2))=sqrt(2)`
Therefore , equation of the circle is
`(x-2)^(2)+(y-0)^(2)=2`
or `x^(2)+y^(2)-4x+2=0`