Since circles touch the lines `x+y=2` and `x-y=2`, centre lies on x-acis or y-axis.
But circle passes through the point `Q(-4,3)`. So, centre lies on negative x-axis.
Let the centre be C(h,0).
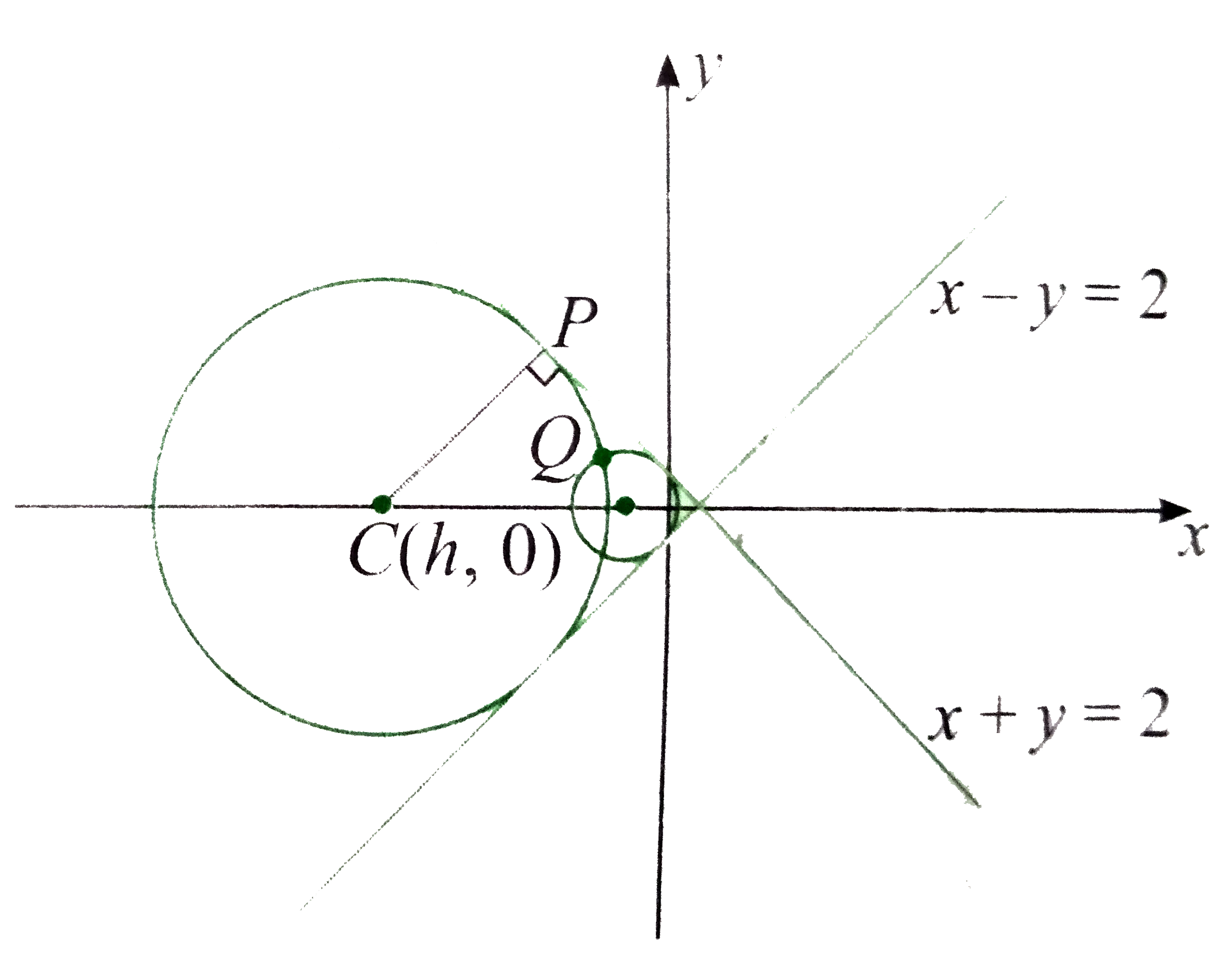
Also, radius, `CP=` distance of centre from the line `x-y=0` ( or `x+y-2=0)`
`=(|h-0-2|)/(sqrt(1^(2)+(-1)^(2)))=(|h-2|)/(sqrt(2))`
Also, radius, `CQ=sqrt((h+4)^(2)+(k-3)^(2))`
`:. CQ=CP`
`implies ((h-2)^(2))/(2)=(h+4)^(2)+(0-3)^(2)`
`implies h=(-20+-sqrt(20^(2)-4(46)))/(2)`
`implies h= -10+-3sqrt(6)`
Thus, equation of the circle is `(x-h)^(2)+y^(2)=((h-2)^(2))/(2)`, where `h= -10+- 3sqrt(6)`