Home
Class 12
MATHS
A circle touches the y-axis at the point...

A circle touches the y-axis at the point (0, 4) and cuts the x-axis in a chord of length 6 units. Then find the radius of the circle.

Text Solution

Verified by Experts

Circles touch the y-axis at point P(0,4).

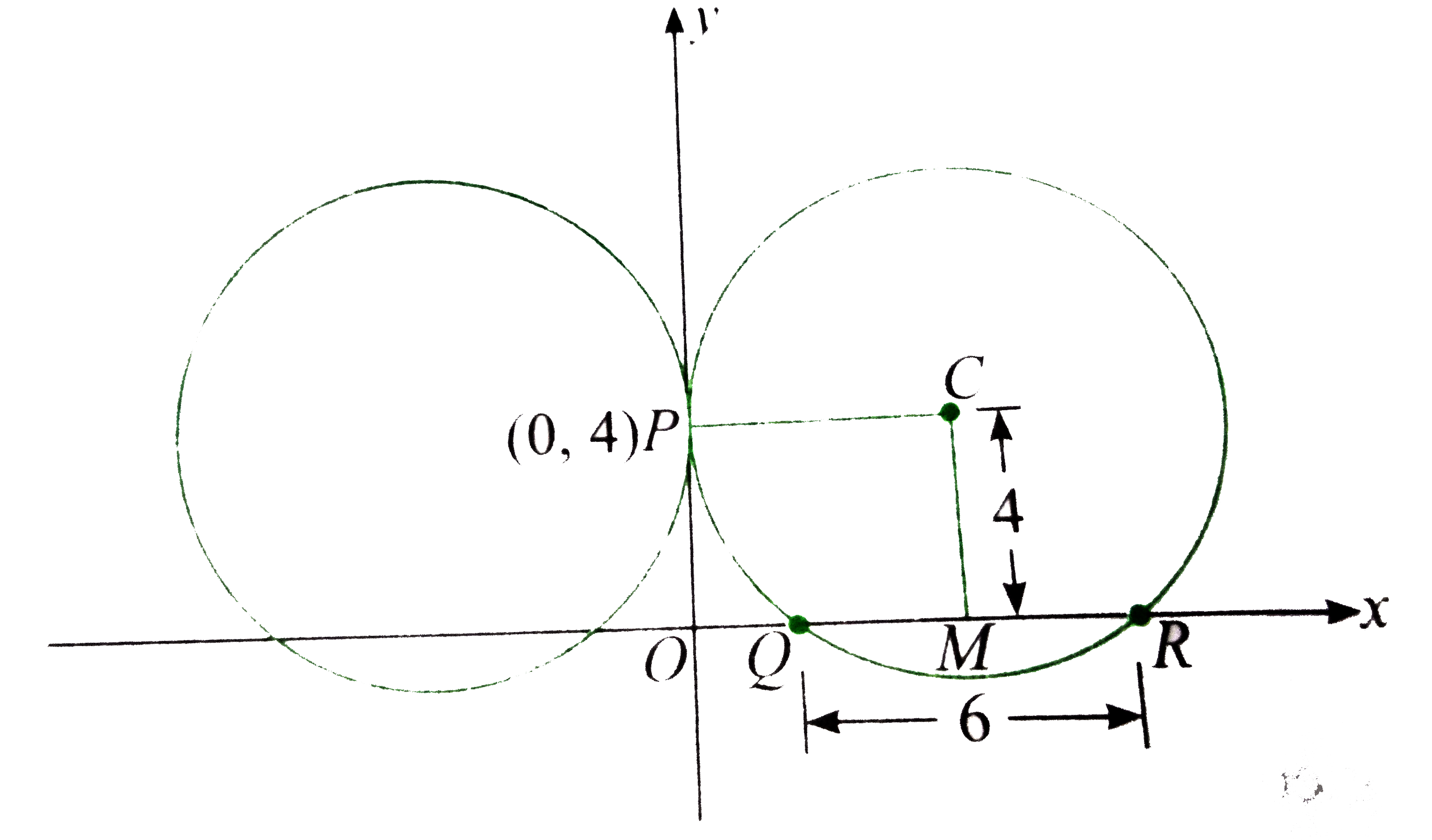
Intercept QR of circle on x-axis is 6 units
`:. QM =3`
Also, C is centre of one of the circles
`:. CM=4`
In triangle CMQ , we have
`CQ^(2)=QM^(2)+CM^(2)=3^(2)+4^(2)`
`:. CQ=5=CP=` radius
Therefore, centre of the circle lying in first quadrant is C(5,4). Thus, equation of circle is `(x-5)^(2)+(y-4)^(2)=25`.
Equation of circle having centre C(-5,4) in secong quadrant is `(x+5)^(2)+(y-4)^(2)=25`.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Find equation of all possible circle that touch the y -axis at the point (0,3) and cut out the chord of length 8 unit from the x - axis .

Find equations of all possible circles that touch the y axis at the point(0,3)and cut the chord of length 8 units from the x axis .

The equations of the circel which touch the x axis at a distance of 3 unit from the origin and intercepts a chord of length 6 unit on the y-axis, aer-

Find the equations to the circles which touch the axis of y at a distance +4 from the origin and intercept a length 6 unit on the axis of x.

Find the equation of the circle which touches the x-axis at a distance +5 unit from the origin and cuts off an intercept of length 24 unit from the y-axis.

A circle touches the X-axis and also touches the circle with centre (0, 3) and radius 2. The locus of the centre of the circle is x^2 = 10y + k , then k = ?

A circle passes through the points (-3, 4), (1, 0) and its centre lies on the x-axis. Find the equation of the circle.

If the lines 3x-4y+4=0 and 6x-8y-7=0 are tangents to a circle, then find the radius of the circle.

A circle passes through the points (-6, 5), (-3, -4) and its radius is 5 unit, find the equation of the circle.

Find the equation of the circle which is touched by y=x , has its center on the positive direction of the x axis and cuts off a chord of length 2 units along the line sqrt(3)y-x=0