Since the circle touches both the aces, its equation takes the form.
`(x-a)^(2)+(y-a)^(2)=a^(2)`
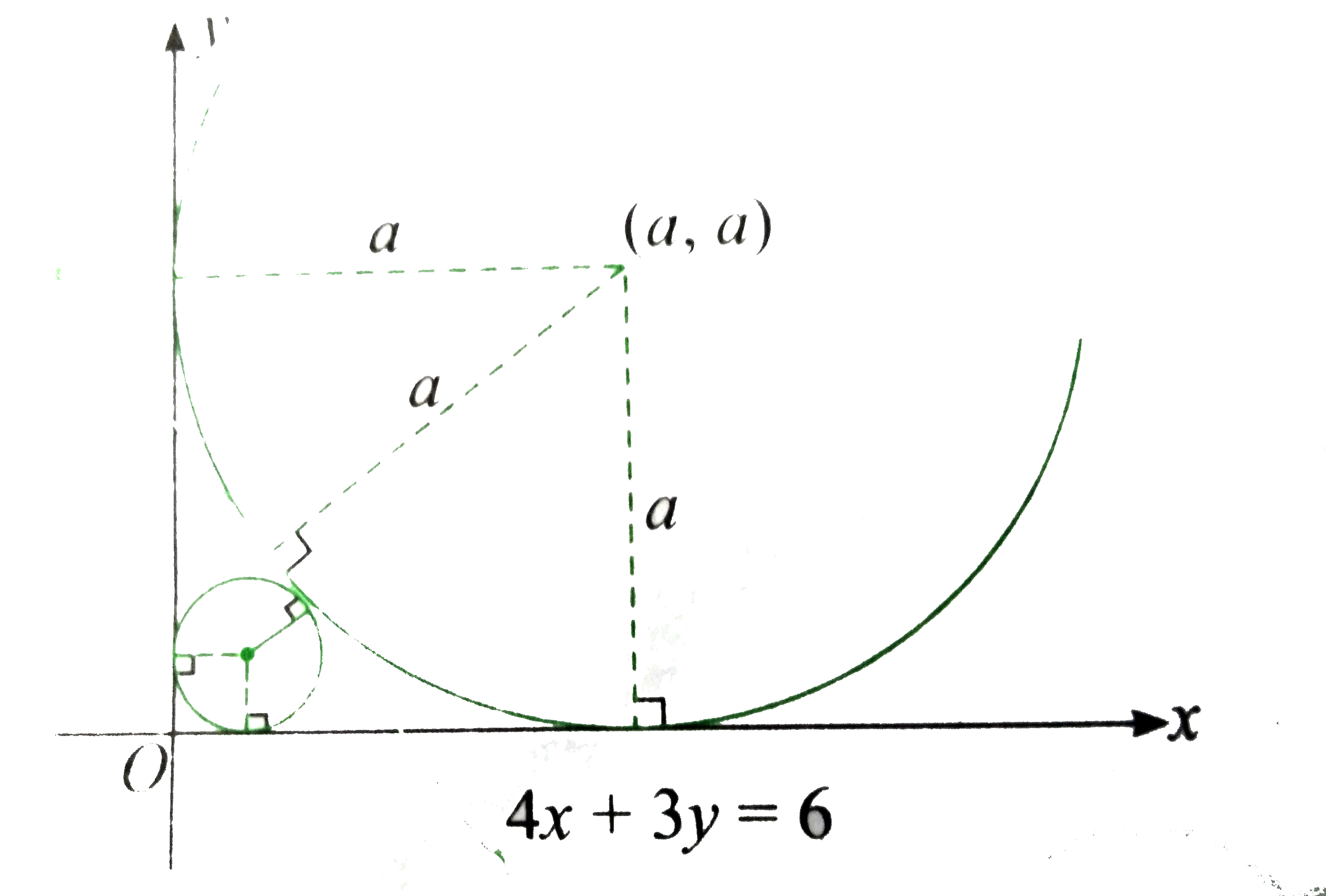
Also, circle touches the line `4x+3y-6=0`
So, the distance of centre of the circle from the line is equatl to its radius.
`:. (|4a+3a-6|)/(sqrt(16+9))=a`
`implies 7a-6= +-5a`
`impliesa=3` or `1//2`
Therefore, possible equatiosn of circle are
`(x-1//2)^(2)+(y-1//2)^(2)=1//4`
and `(x-3)^(2)+(y-3)^(2)=9`