Home
Class 12
MATHS
A variable circle passes through the poi...

A variable circle passes through the point A(a, b) and touches the x-axis. Show that the locus of the other end of the diameter through A is `(x-a)^2 = 4by`

Text Solution

Verified by Experts

As shown in the figure, the variable circle passes through the point A(a,b) and touches the x-axis at ponit P.

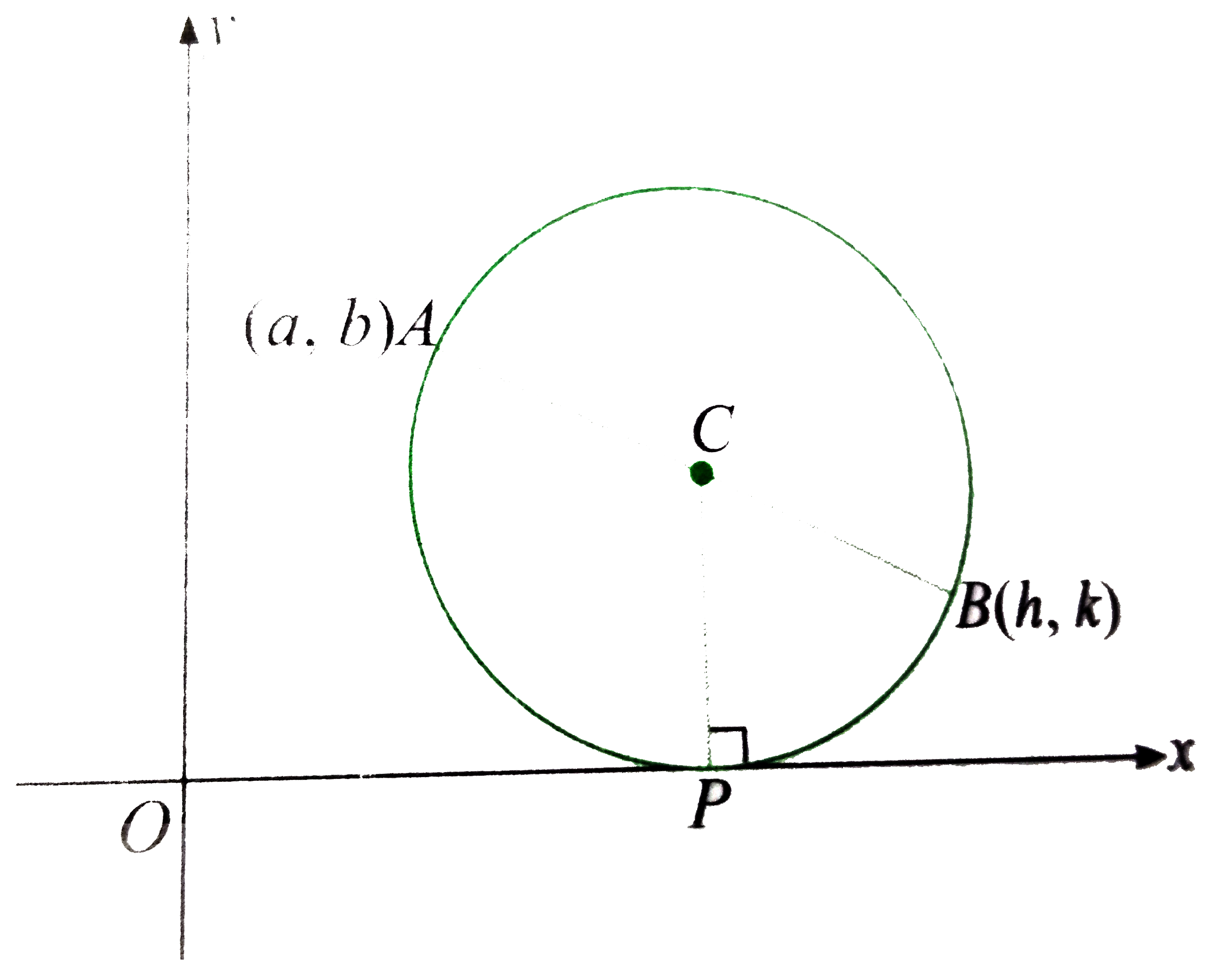
Let the other end of diameter of the circle through A be B(h,k).
So, centre of the circle is `C((h+a)/(2),(k+b)/(2))`
Radius of the circle,` CP=(AB)/(2)`
`implies |(k+b)/(2)|=(sqrt((h-a)^(2)+(k-b)^(2)))/(2)`
Squaring and simplifying, we get `(h-a)^(2)=4bk`.
Therefore, required equation of the locus is `(x-a)^(2)=4by`.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

A variable circle passes through the fixed point A(p,q) and touches the x-axis. The locus of the other end of the diameter through A is-

A variable plane passes through a fixed point (a,b,c) and meets the axes at A ,B ,a n dCdot The locus of the point commom to the planes through A ,Ba n dC parallel to the coordinate planes is

A circle passes through the points (-3, 4), (1, 0) and its centre lies on the x-axis. Find the equation of the circle.

A circle passes through the point (-2, 1) and touches the straight line 3x - 2y = 6 at the point (4, 3) . Find its equation.

The circle passing through (1, - 2) and touching the axis of x at (3, 0) also passes through the point

The circle passing through (-1, 0) and touching the y - axis at (0, 2) also passes through the point

If a circle passes through the point (a, b) and cuts the circle x^2+y^2=K^2 orthogonally then the equation of the locus of its centre is

The circle passing through (1 , -2) and touching the axis of x at (3 , 0) also passes through the point _

A variable line passes through the fixed point (alpha,beta) . The locus of the foot of the perpendicular from the origin on the line is,

A variable plane passes through a fixed point (a ,b ,c) and cuts the coordinate axes at points A ,B ,a n dCdot Show that locus of the centre of the sphere O A B Ci s a/x+b/y+c/z=2.