Home
Class 12
MATHS
A point moves so that the sum of the squ...

A point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.

Text Solution

Verified by Experts


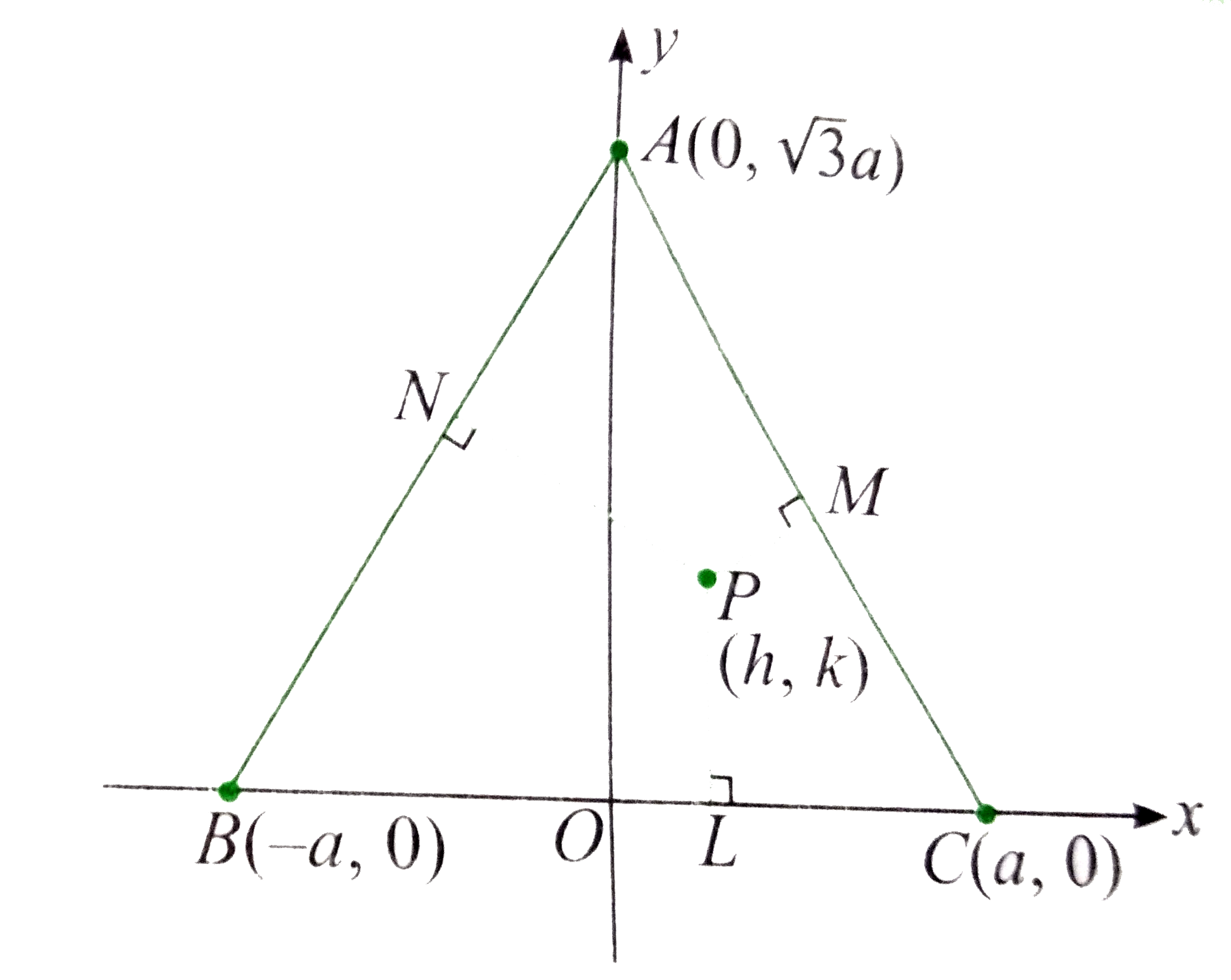
Let vertices B and C of equilateral triangle be (-a,0) and (a,0)
`OA=OB tan 60^(@)=a sqrt(3)`
`:. A -= (0,asqrt(3))`
Let point P be (h,k).
Equations of AC and BC are `xsqrt(3)+y-asqrt(3)=0` and `xsqrt(3)-y+asqrt(3)=0`, respectively.
According to the question,
`PL^(2)+PM^(2)+PN^(2)=` constant (say `lambda)`
`:. k^(2)+((sqrt(3)h+k-sqrt(3)a)/(2))^(2)+((sqrt(3)h-k+sqrt(3)a)/(2))^(2)=lambda`
`implies 6h^(2)+6k^(2)-4sqrt(3)ak+6a^(2)-4 lambda=0`
Hence, the required locus is `6x^(2)+6y^(2)-4sqrt(3)ay+6a^(2)-4 lambda =0` which is a circle
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

A point moves so that sum of the squares of its distances from the vertices of a triangle is always constant. Prove that the locus of the moving point is a circle whose centre is the centroid of the given triangle.

Prove that the locus of the point that moves such that the sum of the squares of its distances from the three vertices of a triangle is constant is a circle.

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals

A straight line moves so that the product of the length of the perpendiculars on it from two fixed points is constant. Prove that the locus of the feet of the perpendiculars from each of these points upon the straight line is a unique circle.

A point moves so that the distance between the foot of perpendiculars from it on the lines a x^2+2hx y+b y^2=0 is a constant 2d . Show that the equation to its locus is (x^2+y^2)(h^2-a b)=d^2{(a-b)^2+4h^2}dot

A point moves so that the sum of squares of its distances from the points (1, 2) and (-2, 1) is always 6. Then its locus is

A point moves so that the sum of squares of its distances from the points (1, 2) and (-2,1) is always 6. Then its locus is

A point moves so that the sum of squares of its distances from the points (1,2) and (-2,1) is always 6 . Then its locus is _

Prove that the sum of the perpendiculars drawn from any interior point of an equilateral triangle to its sides then sum of three perpendiculars is equal to the altitude of the triangle.

A point moves in such a manner that the sum of the squares of its distances from the origin and the point (2, -3) is always 19. Show that the locus of the moving point is a circle. Find the equation to the locus.