The point on a circle nearest to the point `P(2,1)` is at a distance of 4 units and the farthest point is (6, 5). Then find the equation of the circle.

Explanation

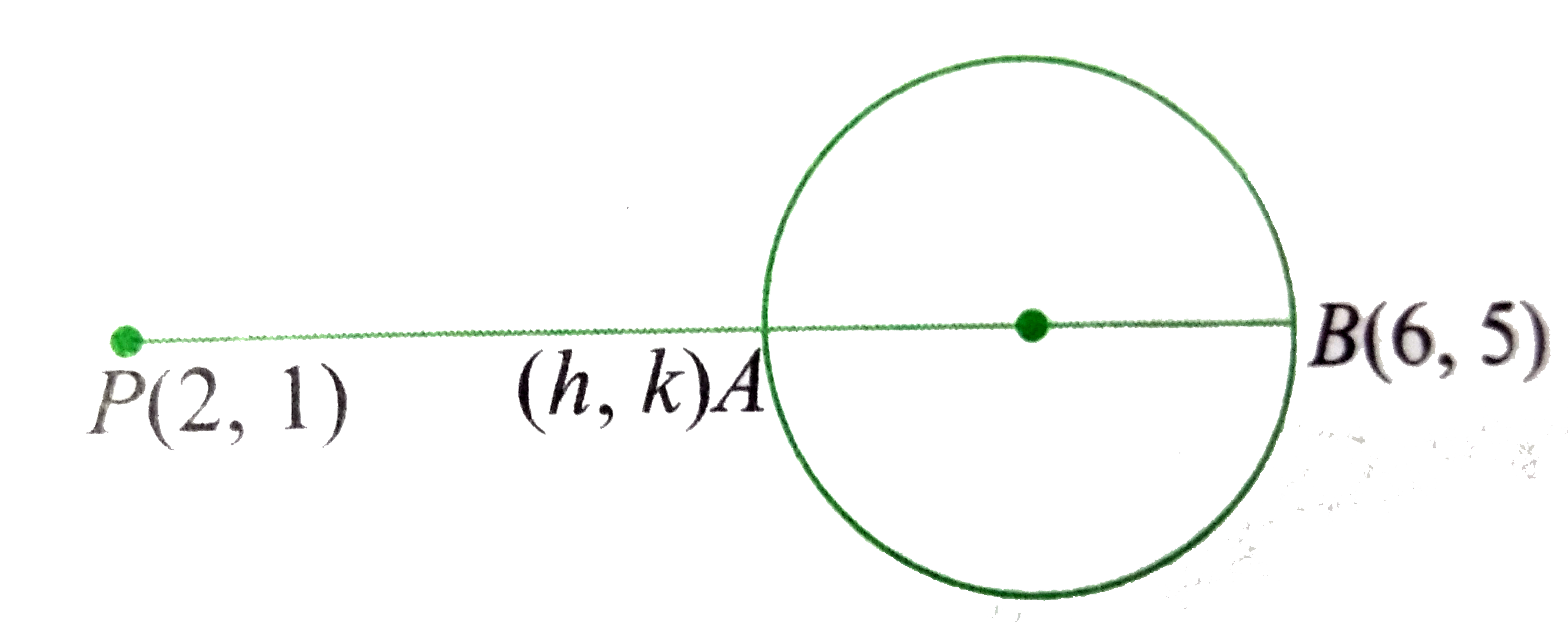
In the figure, point nearest to P(2,1) on the circle is A(h,k) such that AP`=4` units.
Also, point B(6,5) is on the circle which is farthest point from P. Clearly, AB is diameter of the circle.
Now, `PB=sqrt((6-2)^(2)+(5-1)^(2))=4sqrt(2)`
`:. AB=PB-PA=4(sqrt(2)-1)`
Thus, `(AB)/(AP)=(sqrt(2)-1)/(1)`
`:. A=((6-2(sqrt(2)-1))/(1+(sqrt(2)-1)),(5+1(sqrt(2)-1))/(1+(sqrt(2)-1)))`
`=(2+2sqrt(2),1+2sqrt(2))`
Hence, equation of circle having AB as diameter is
`(x-6)(x-2-2sqrt(2))+(y-5)(y-1-2sqrt(2))=0`