Home
Class 12
MATHS
A circle with center at the origin and r...

A circle with center at the origin and radius equal to a meets the axis of `x` at `Aa n dB. P(alpha)` and `Q(beta)` are two points on the circle so that `alpha-beta=2gamma` , where `gamma` is a constant. Find the locus of the point of intersection of `A P` and `B Qdot`

Text Solution

Verified by Experts

Let

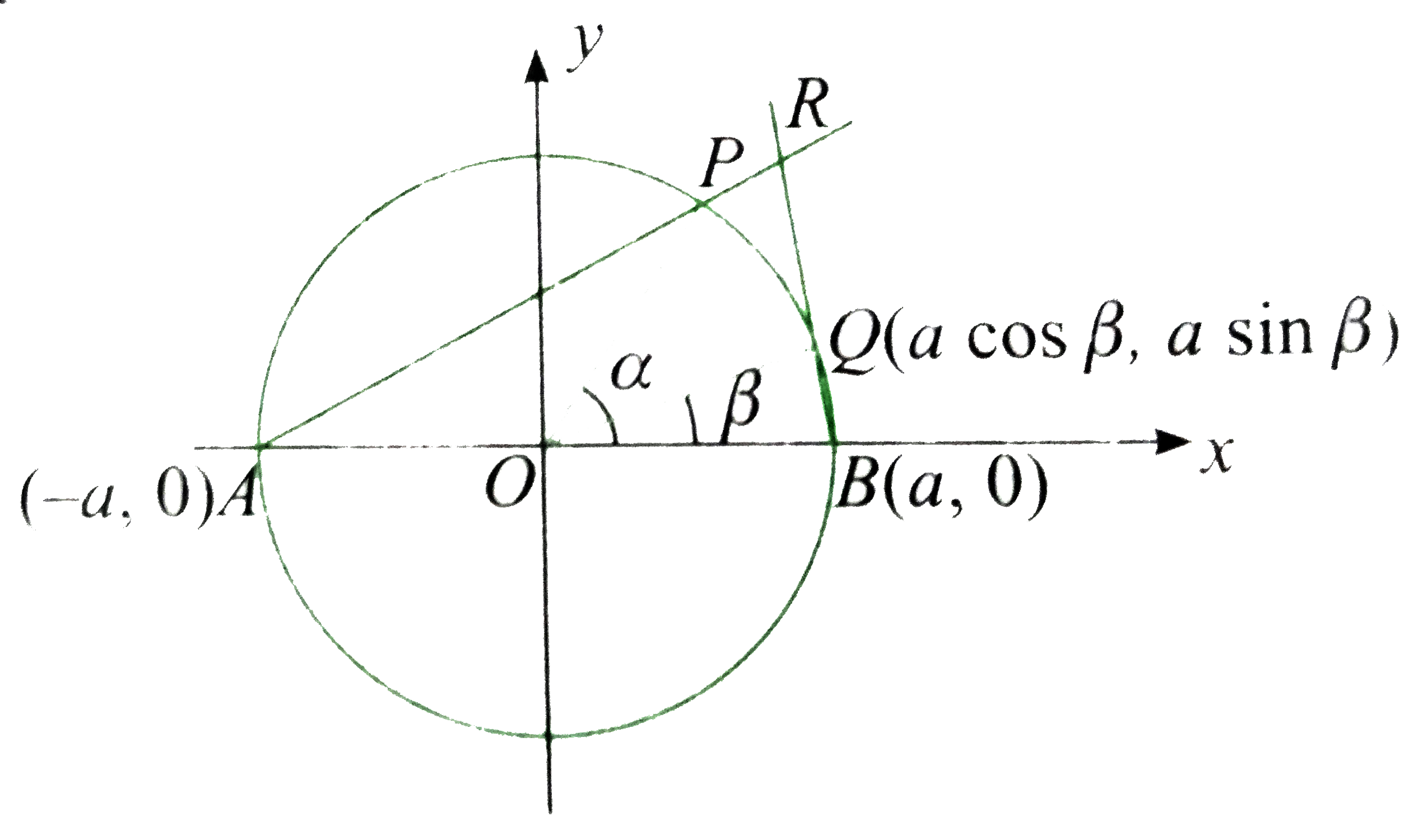
The coordinates of A are ( -a,0) and that of P are `(a cos alpha, a sin alpha)`.
Therefore, the equation of AP is
`y=(a sin alpha)/(a(cos alpha+1))(x+a)`
or `y=tan.(alpha)/(2)(x+a)` (1)
Similarly, the equationof BQ is
`y=( a sin beta)/(a(cos beta-1))(x-a)`
or `y=- cot . (beta)/(2)(x-a)` (2)
We now eliminate `alpha` and `beta` from (1) and (2). Therefore,
`tan.(alpha)/(2)=(y)/(a+x),tan.(beta)/(2)=(a-x)/(y)`
Now, `alpha-beta=2gammaimpliesgamma=(alpha)/(2)-(beta)/(2)`
`:. tan gamma=(tan.(alpha)/(2)-tan.(beta)/(2))/(1+tan.(alpha)/(2)tan.(beta)/(2))=((y)/(a+x)-(a-x)/(y))/(1+(y)/(a+x).(a-x)/(y))`
or `tan gamma=(y^(2)-(a^(2)-x^(2)))/((a+x)y+(a-x)y)`
`=(x^(2)+y^(2)-a^(2))/(2ay)`
or `x^(2)+y^(2)-2ay tan gamma=a^(2)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

Two variable chords A Ba n dB C of a circle x^2+y^2=r^2 are such that A B=B C=r . Find the locus of the point of intersection of tangents at Aa n dCdot

Find the equation to the circle which touches the y-axis at the origin and passes through the point (alpha, beta) .

P(a,5a) and Q(4a,a) are two points. Two circles are drawn through these points touching the axis of y. Centre of these circles are at

Ankita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that angle AQC= angle BQD .

S is a circle having the center at (0,a) and radius b(b < a)dot A variable circle centered at (alpha,0) and touching the circle S meets the X-axis at Ma n dN . Find the a point P on the Y-axis, such that /_M P N is a constant for any choice of alpha

If P is any point on the plane l x+m y+n z=pa n dQ is a point on the line O P such that O P.O Q=p^2 , then find the locus of the point Qdot

Let x-ysin alpha-zsin beta=0 , xsin alpha+zsin gamma-y=0 and xsin beta+ysin gamma-z=0 be the equations of the planes such that alpha+beta+gamma=pi//2 (where alpha,beta and gamma!=0)dot Then show that there is a common line of intersection of the three given planes.

If the axis are transferred to parallel axis throught the point (alpha,beta) , then equation of the circle (x-alpha)^(2)+(y-beta)^(2)=a^(2) reduces to the form-

A line passing through the origin O(0,0) intersects two concentric circles of radii aa n db at Pa n d Q , If the lines parallel to the X-and Y-axes through Qa n dP , respectively, meet at point R , then find the locus of Rdot

If (alpha ,beta) is a point on the circle whose centre is on the x-axis and which touches the line x+y=0 at (2,-2), then the greatest value of 'alpha' is :