`P` is the variable point on the circle with center at `C. C A` and `C B` are perpendiculars from `C` on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle `P A B` is a circle with center at the centroid of triangle `C A B` and radius equal to the one-third of the radius of the given circle.

Explanation

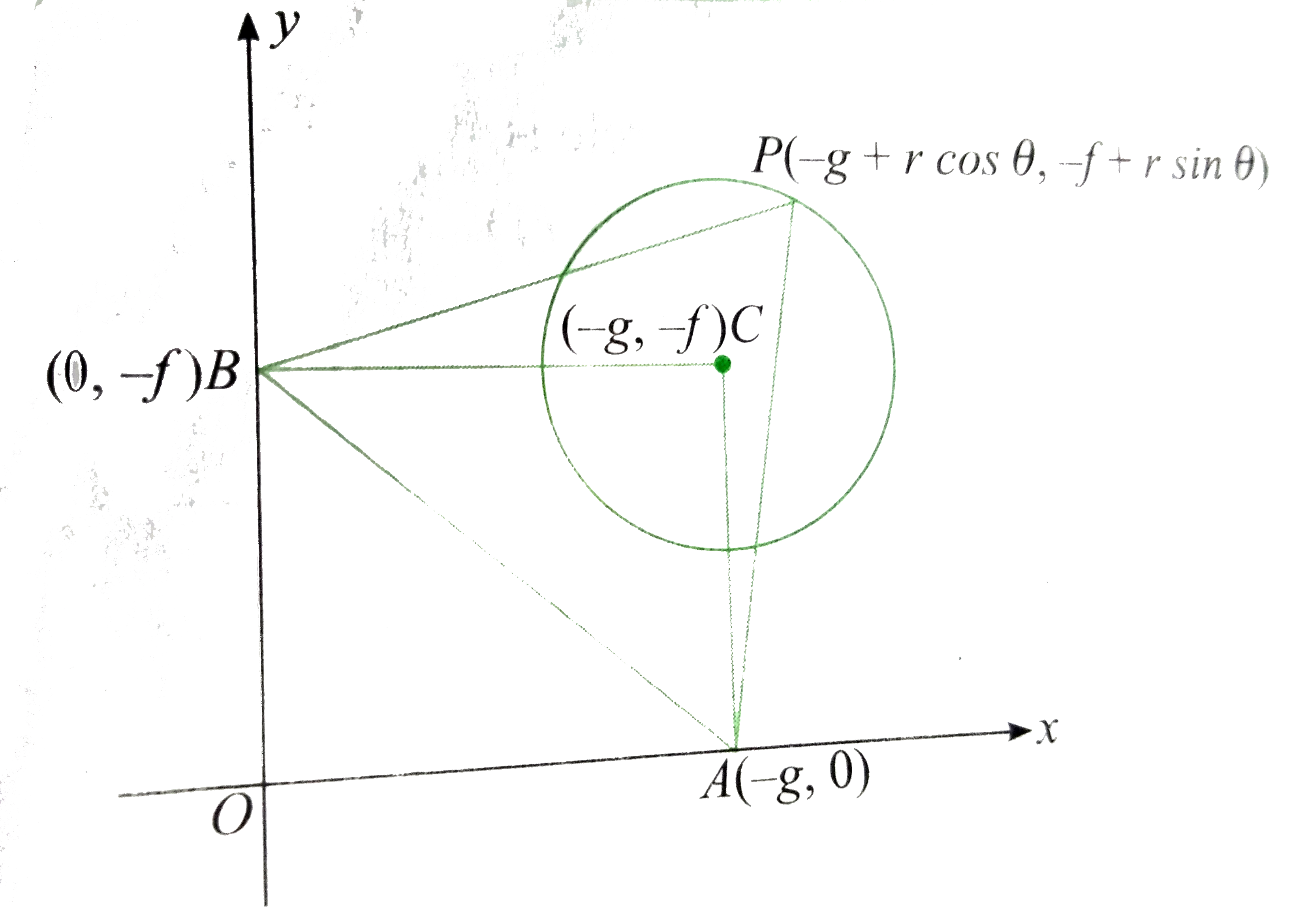
Let the circle be `x^(2)+y^(2)+2gx+2fy+c=0`.
Let the centroid of triangle PAB be (h,k). ltBRgt `:. 3h=2g+r cos theta`
and `3k= -2f+r sin theta`
`implies (2h+2g)^(2)+(3k+2f)^(2)=r^(2)`
`implies (x+2g//3)^(2)+(y+2//3)^(2)=r^(2)//9`
This is the required locus which is a circle.
Centre of the circle is `(-2g//3,-2f//3)` which is centroid of the triangle CAB and radius `(r//3)` which is one-third of the radius of the given circle.