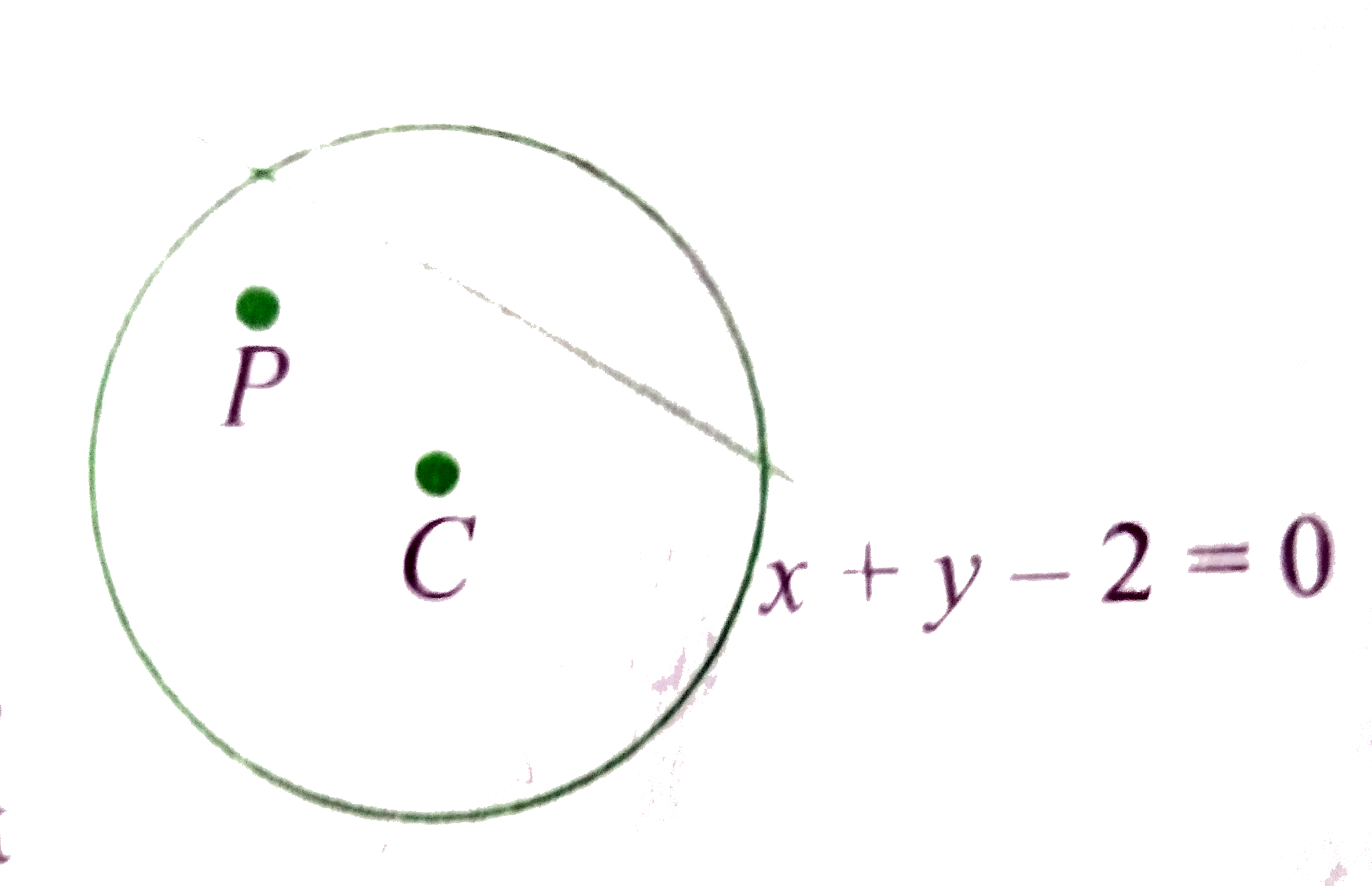The given circle
`S(x,y)-=x^(2)+y^(2)-x-y-6=0` (1) has center at `C-= (1//2, 1//2)`,
According to the required conditions, the given point `P(alpha-1,alpha+1)` must lie inside the given circle, i.e.,
`S(alpha-1,alpha+1)lt0`
or `(alpha-1)^(2)+(alpha+1)^(2)-(alpha-11)-(alpha+1)-6 lt0`
or `alpha^(2)-alpha-2 lt0`
i.e., `(alpha-2)(alpha+1) lt0`
or `-1 ltalpha lt 2` (2)
Also, P and C must lie on the same side of the line
`L(x,y)-= x+y-2=0` (3)
i.e., `L(1//2,1//2)` and `L (alpha-1,alpha+1)` must have the same sign.
Now, since
`L((1)/(2),(1)/(2))=(1)/(2)+(1)/(2)-2lt0`
we have `L(alpha-1,alpha+1)=(alpha-1)+(alpha+1)-2lt0`
i.e., `alpha lt 1` (4)
Inequalities (2) and (4) together give the possible values of `alpha` as `-1 lt alpha lt 1`