Home
Class 12
MATHS
The circle x^2+y^2-6x-10 y+k=0 does not ...

The circle `x^2+y^2-6x-10 y+k=0` does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of `kdot`

Text Solution

Verified by Experts

The equation of the circle is
`x^(2)+y^(2)-6x-10y+k=0` (1)
whose center is C(3,5) and radius

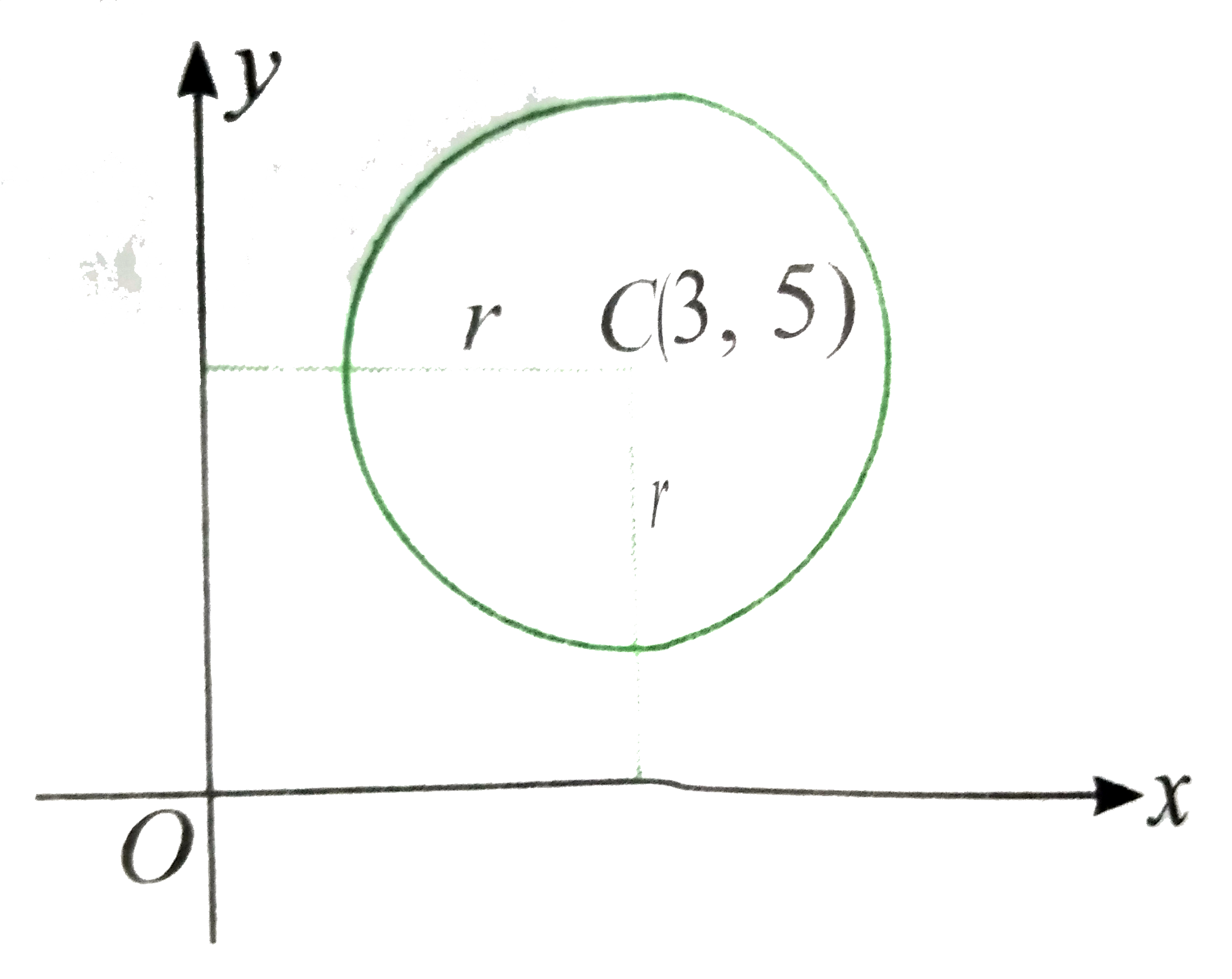
`r=sqrt(34-k)`
If the circle does not touch or intersect the x-axis, then radius
`r lt y` coordinate of center C
or `sqrt(34-k)lt5`
or `34-klt25`
or `kgt9` (2)
Also, if the circle does not touch or intersect the y-axis, then the radius
`r lt x-` coordinate of center C
or `sqrt(34-k) lt3`
or `34 -k lt9`
or `kgt 25` (3)
If the point (1,4) is inside the circle, then
Its distance from center `C ltr`
or `sqrt((3-2)^(2)+(5-4)^(2))lt sqrt(34-k)`
or `5 lt34 -k`
or `klt29` (4)
Now, all the conditions (2),(3), and (4) are satisfied if `25 lt k lt29` which is the required range of the values of k.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

The circle x^2+y^2-2x-2y+k=0 represents a point circle when k.=

The circle x ^(2) +y^(2) -8 x+4=0 touches -

Show that the circle x^(2) + y^(2) + 6(x-y) + 9 = 0 touches the coordinates axes. Also find the equation of the circle which passes through the common points of intersection of the above circle and the straight line x-y+4 = 0 and which also passes through the origin.

Tangent drawn from the point P(4,0) to the circle x^2+y^2=8 touches it at the point A in the first quadrant. Find the coordinates of another point B on the circle such that A B=4 .

Show that the circle x^(2) + y^(2) + 4(x+y) + 4 = 0 touches the coordinates axes. Also find the equation of the circle which passes through the common points of intersection of the above circle and the straight line x+y+2 = 0 and which also passes through the origin.

Show that the circles x^2+y^2-10 x+4y-20=0 and x^2+y^2+14 x-6y+22=0 touch each other. Find the coordinates of the point of contact and the equation of the common tangent at the point of contact.

If a circle passes through the points of intersection of the coordinates axes with the lines lambdax-y+1=0 and x-2y+3=0 , then find the value of lambda .

If the length tangent drawn from the point (5, 3) to the circle x^2+y^2+2x+k y+17=0 is 7, then find the value of kdot

The circle x^(2) + y^(2) + 2x - 4y - 11 = 0 and the line x-y+1=0 intersect at A and B. Find the equation to the circle on AB as diameter.

The number of integral coordinates of the points (x, y) which are lying inside the circle x^(2) + y^(2) = 25 is n, then the integer value of (n)/(9) will be -