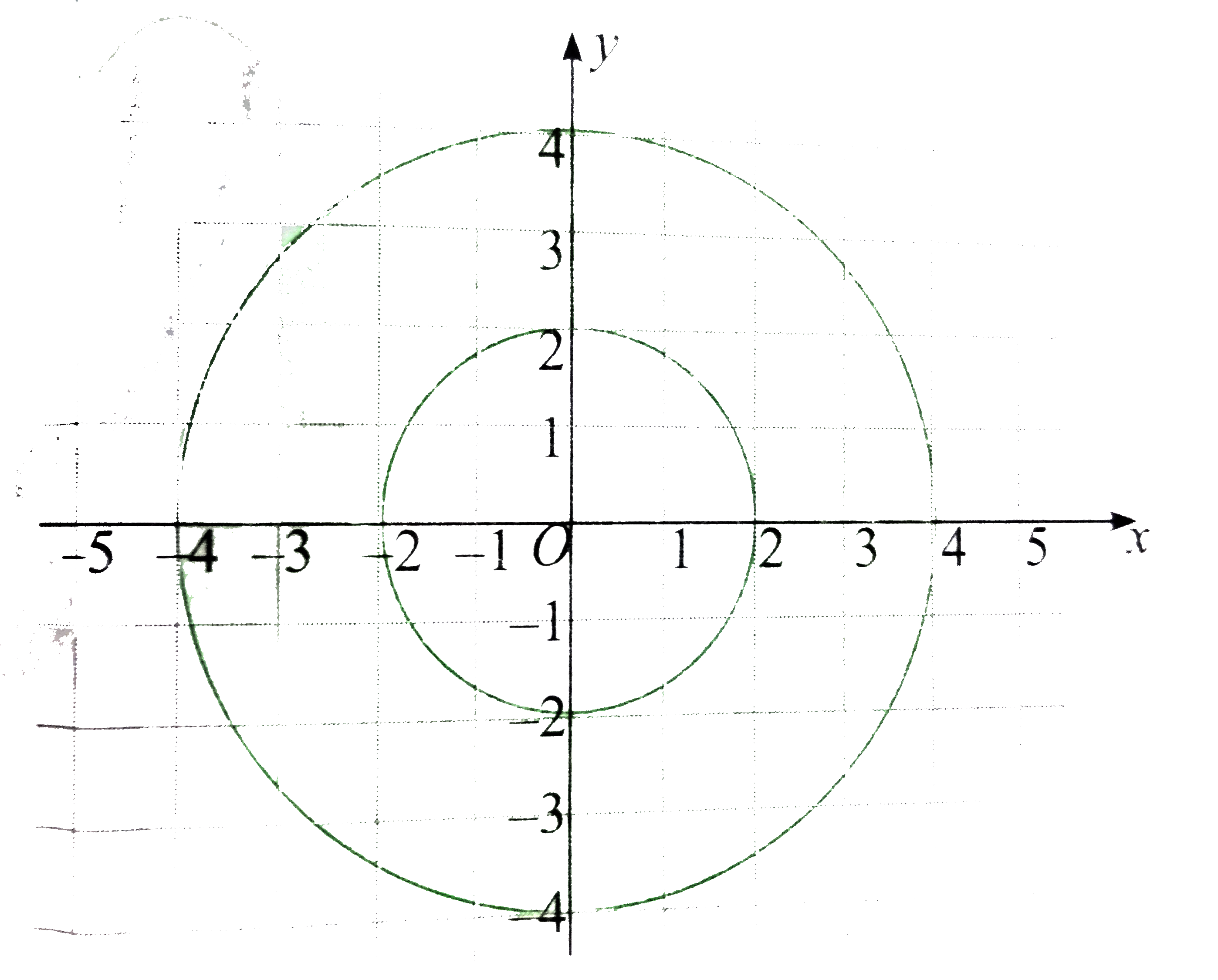
The points satisfying `4 lt x^(2)+y^(2)lt16` lie in the region outside the circle `x^(2)+y^(2)=4` and inside the circle `x^(2)+y^(2)=16` as shown in the following figure.
Now, `3x^(2)-y^(2) gt0`
`:. (sqrt(3)x-y)(sqrt(3)x+y)gt0`
Now, draw the lines `sqrt(3)x-y=0` and `sqrt(3)x+y=0`.
Therefore, `3x^(2)-y^(2)gt0` represents the following region `:`
Hence, the region of the points satisfying both the inequalities is shown in the following figure.
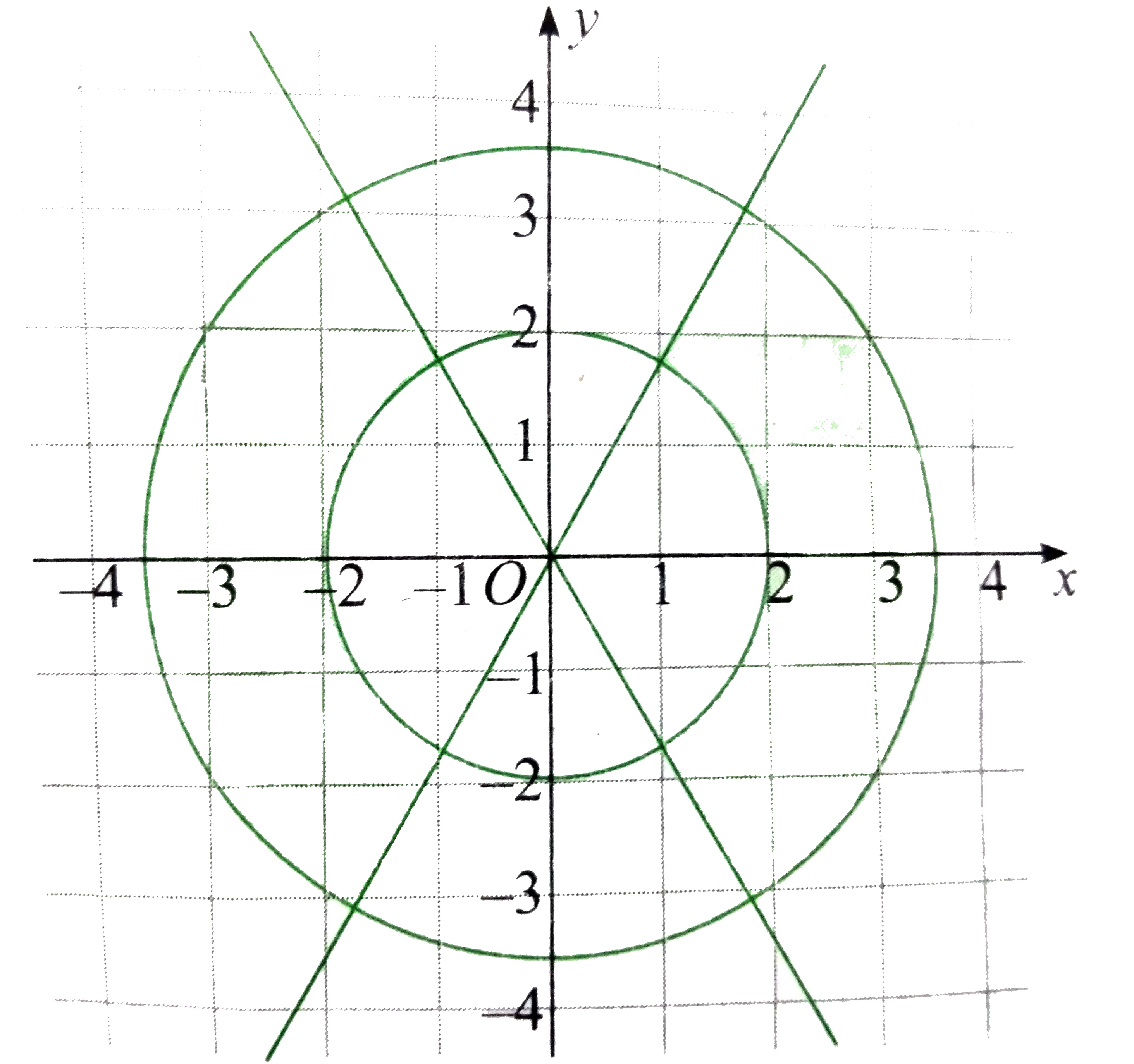
Hence, the required area is
`(4)/(6)[pi(4)^(2)-pi(2)^(2)]=8 pi`