Home
Class 12
MATHS
If from any point P on the circle x^2+y^...

If from any point `P` on the circle `x^2+y^2+2gx+2fy+c=0,` tangents are drawn to the circle `x^2+y^2+2gx+2fy+csin^2alpha+(g^2+f^2)cos^2alpha=0` , then find the angle between the tangents.

Text Solution

Verified by Experts

Given circles are `x^(2)+y^(2)+2gx+2fy+c=0` (1)
and `x^(2)+y^(2)+2gx+2fy+c sin ^(2)alpha+(g^(2)+f^(2))cos^(2)alpha=0` (2)

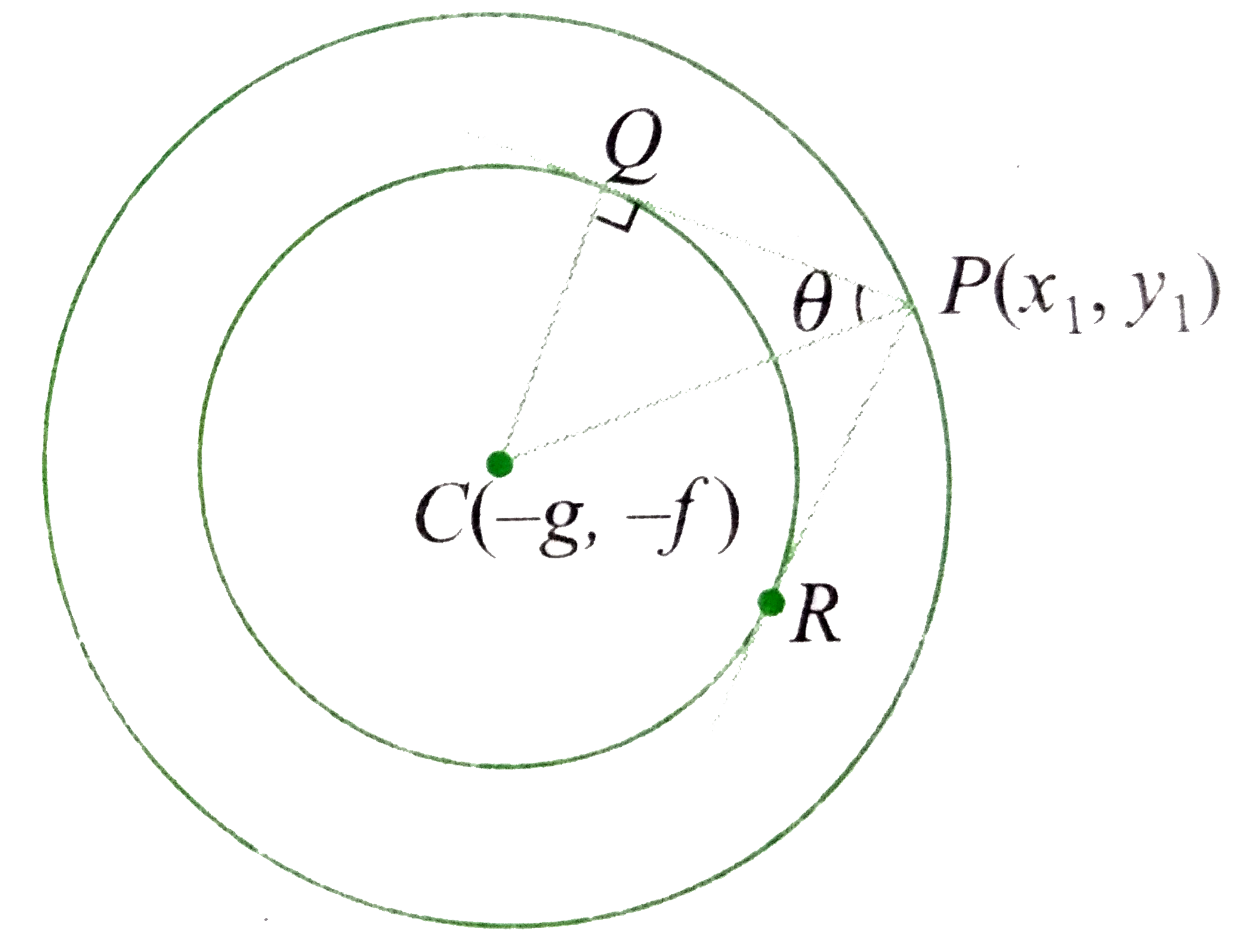
Let `P(x_(1),y_(1))` be a point on the circle (1).
`:. x_(1)^(2)+y_(1)^(2)+2gx_(1)+2fy_(1)+c=0` (3)
The length of the tangent drawn from `P(x_(1),y_(1))` to the circle (2) is
`PQ=sqrt(x_(1)^(2)+y_(1)^(2)+2gx_(1)+2fy_(1)+csin^(2)alpha+(g+f^(2))cos^(2)alpha)`
`=sqrt(-c+csin^(2)alpha+(g^(2)+f^(2))cos^(2)alpha))` (Using (1))
`=(sqrt(g^(2)+f^(2)-c))cosalpha`
The radius of the circle (2) is
`CQ=(sqrt(g^(2)+f^(2)-csin^(2)alpha-(g^(2)+f^(2))cos^(2)alpha)`
`=(sqrt(g^(2)+f^(2)-c))sin alpha`
In `Delta CPQ`
`tan theta=(CQ)/(PQ)=(sqrt(g^(2)+f^(2)-c)sinalpha)/(sqrt(g^(2)+f^(2)-c)cosalpha)=tan alpha`
`:. theta= alpha`
Therefore, angle between tangents is `2 alpha`.
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

From an arbitrary point P on the circle x^2+y^2=9 , tangents are drawn to the circle x^2+y^2=1 , which meet x^2+y^2=9 at A and B . The locus of the point of intersection of tangents at A and B to the circle x^2+y^2=9 is (a) x^2+y^2=((27)/7)^2 (b) x^2-y^2((27)/7)^2 (c) y^2-x^2=((27)/7)^2 (d) none of these

Tangents are drawn from any point on the circle x^(2)+y^(2) = 41 to the ellipse (x^(2))/(25)+(y^(2))/(16) =1 then the angle between the two tangents is

If the tangents are drawn to the circle x^2+y^2=12 at the point where it meets the circle x^2+y^2-5x+3y-2=0, then find the point of intersection of these tangents.

A pair of tangents are drawn from the origin to the circle x^2+y^2+20(x+y)+20=0 . Then find its equations.

Tangents are drawn to the parabola (x-3)^2+(y+4)^2=((3x-4y-6)^2)/(25) at the extremities of the chord 2x-3y-18=0 . Find the angle between the tangents.

The tangents drawn from the origin x^2+y^2+2gx+2fy+f^2=0 are perpendicular if

The length of the tangent drawn from any point on the circle x ^(2) +y^(2) +2gx+2fy+c_(1) =0 to the circel x ^(2)+y^(2) +2gx+2fy+c_(2) =0 is-

The equation x^2+y^2+2gx+2fy+c=0 represents a point -circle when

Find the area of an equilateral triangle inscribed in the circle x^2 + y^2 + 2gx + 2fy + c = 0

The angle between a pair of tangents drawn from a point P to the circle x^2+y^2+4x-6y+9sin^2alpha+13cos^2alpha=0" is "2alpha . The equation of the locus of the point P is