Two parallel tangents to a given circle are cut by a third tangent at the point `Ra n dQ` . Show that the lines from `Ra n dQ` to the center of the circle are mutually perpendicular.

Explanation

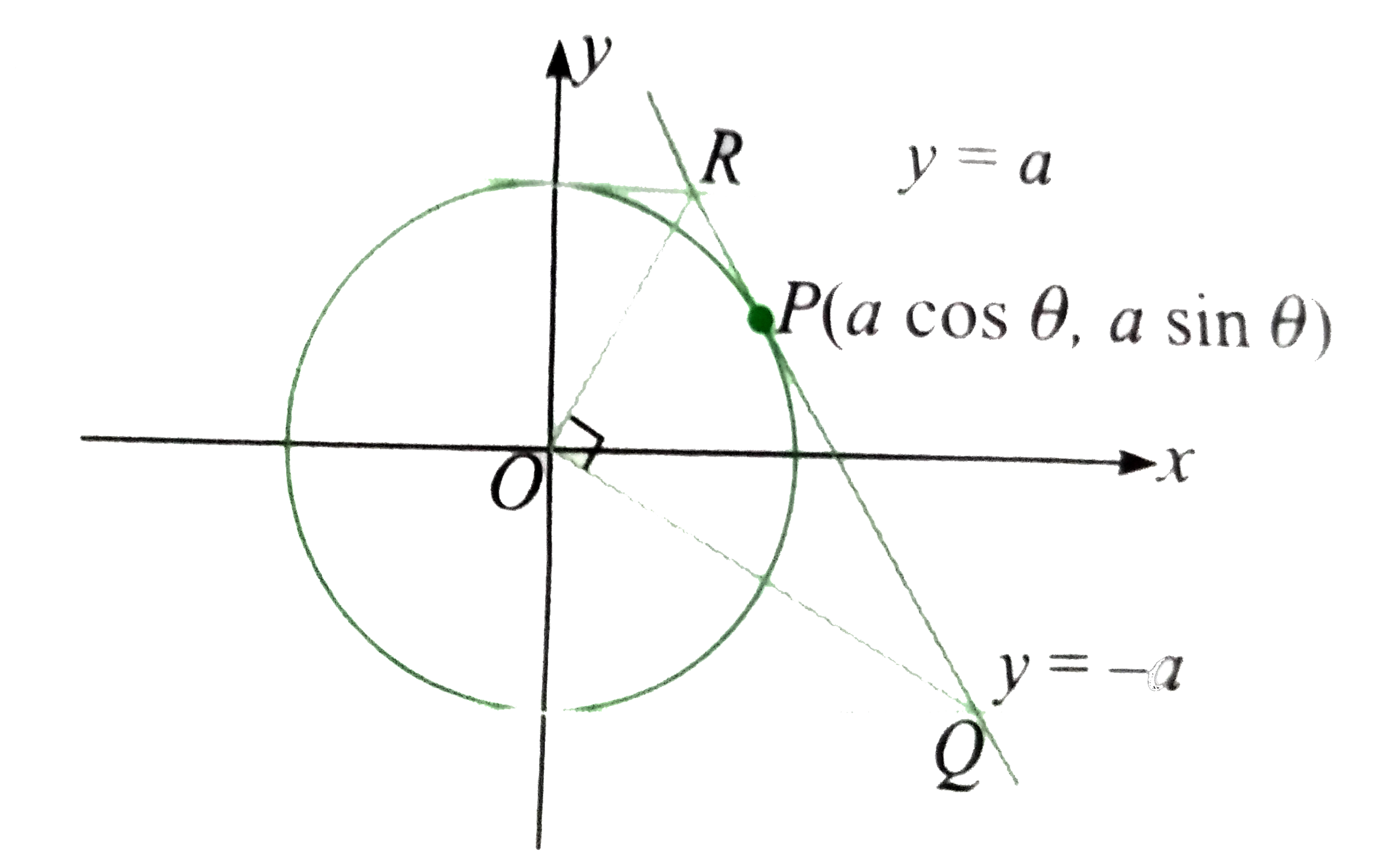
Consider the circle `x^(2)+y^(2)=a^(2)`.
Let the two parallel tangents be `y=a ` and `y=-a`.
Third tangent at point `P(a cos theta, a sin theta ) ` is `cos theta x +sin theta y=a`.
Solving these with `y=+- a, ` we get `x=(a overset(-)(+)asin theta)/(cos theta)`
`:. R-=((a-asin theta)/(cos theta),a) ` and `Q -=((a+a sin theta)/(cos theta),-a)`
Slope of OR, `m_(1)=(a)/((a-a sin theta)/(cos theta))=(cos theta)/(1-sin theta)`
Slope of OQ, `m_(2)=(-a)/((a+a sin theta)/(cos theta))=-(cos theta)/(1+sin theta)`
`m_(1)xxm_(2)=(cos theta)/(1-sin theta)xx(-(cos theta)/(1+sin theta))=-(cos^(2)theta)/(1-sin^(2)theta)=-1`
Thus, QR subtends right angle at centre.