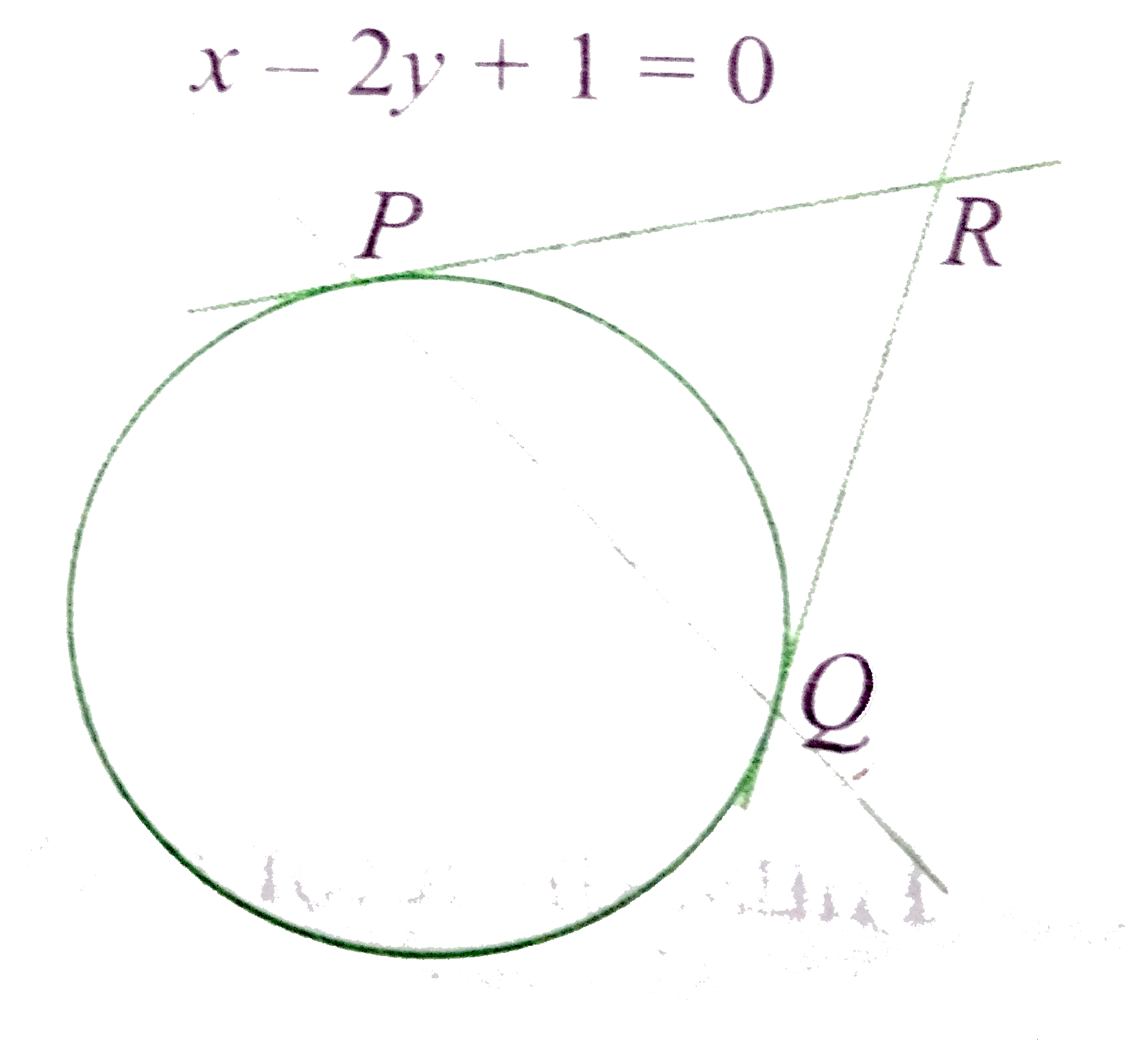Home
Class 12
MATHS
If the straight line x=2y+1=0 intersects...

If the straight line `x=2y+1=0` intersects the circle `x^2+y^2=25` at point `Pa n dQ` , then find the coordinates of the point of intersection of the tangents drawn at `Pa n dQ` to the circle `x^2+y^2=25.`

Text Solution

Verified by Experts

Let R(h,k) be the point of intersection of the tangents drawn at P and Q to the given circle. Then PQ is the chord of the cord of tangents drawn from R to `x^(2)+y^(2)=25`
So, its equation is
`hx+ky-25=0` (1)
It is given that the eqation of PQ is
`x-2y+1=0` (2)
Since (1) and (2) represent the same line, we have
`(h)/(1)=(k)/(-2)=(-25)/(1)`
or `h=-25,k=50 `
Hence, the required point is `(-25,50)`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

If the straight line x - 2y + 1 = 0 intersects the circle x^2 + y^2 = 25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x^2 + y^2 = 25 .

Find the point(s) of intersection of the line 2x + 3y = 18 and the circle x^2 + y^2 = 25

Find the locus of the point of intersection of the perpendicular tangents of the curve y^2+4y-6x-2=0 .

Obtain the locus of the point of intersection of the tangent to the circle x^2 + y^2 = a^2 which include an angle alpha .

If the tangents are drawn to the circle x^2+y^2=12 at the point where it meets the circle x^2+y^2-5x+3y-2=0, then find the point of intersection of these tangents.

Find the equation of the smallest circle passing through the point of intersection of the line x+y=1 and the circle x^(2)+y^(2)=9 .

Find the lengths of the tangents drawn from the point. (-1,1) to the circle x^(2)+y^(2)-2x+4y+1=0

From an arbitrary point P on the circle x^2+y^2=9 , tangents are drawn to the circle x^2+y^2=1 , which meet x^2+y^2=9 at A and B . The locus of the point of intersection of tangents at A and B to the circle x^2+y^2=9 is (a) x^2+y^2=((27)/7)^2 (b) x^2-y^2((27)/7)^2 (c) y^2-x^2=((27)/7)^2 (d) none of these

Find the condition for which the lines joining the origin to the points of intersection of the line y= mx+c and the circle x^2+y^2=a^2 will be mutually bot

If line x-2y-1=0 intersects parabola y^(2)=4x at P and Q, then find the point of intersection of normals at P and Q.