Required circle through proint A(4,3) touches the circle `S_(1) -= x^(2)+y^(2)=1`.
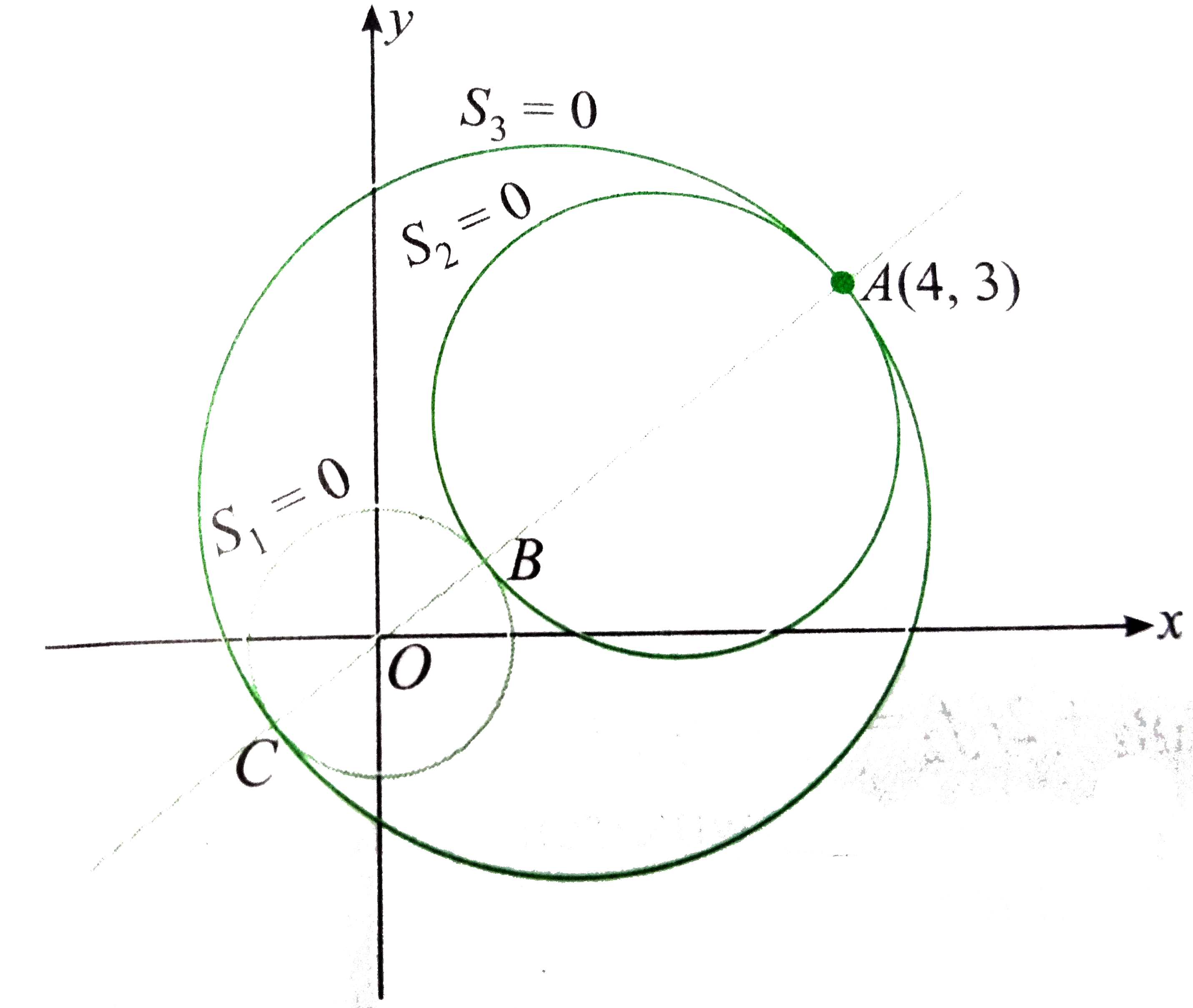
This circle is smallest if it touches the given circle externally and point of contact B lies on the common normal.
Equation of line OA is `y=(3)/(4) x` (1)
Putting this value of y from (1) in `x^(2)+y^(2)=1` , we get
`x=+-(4)?(5)` and `y=+- (3)/(5)`
`:. B=((4)/(5),(3)/(5))`
and `C=((-4)/(5),(-3)/(5))`
Therefore, equation of circle with AB as diameter is
`S_(2) -= (x-(4)/(5))(x-4)+(y-3)(y-(3)/(5))=0`
or `x^(2)+y^(2)-(24)/(5)x-(18)/(5)y=0`
Required circle is the largenst if given circle touches given circle internally and point of contact C lies on the common normal.
Therefore, equation of circle with AC as diameter is
`S_(3)=(x+(4)/(5))(x-4)+(y+(3)/(5))(y-3)=0`
or `x^(2)+y^(2)-(16)/(5)x-(12)/(5)y-5=0`