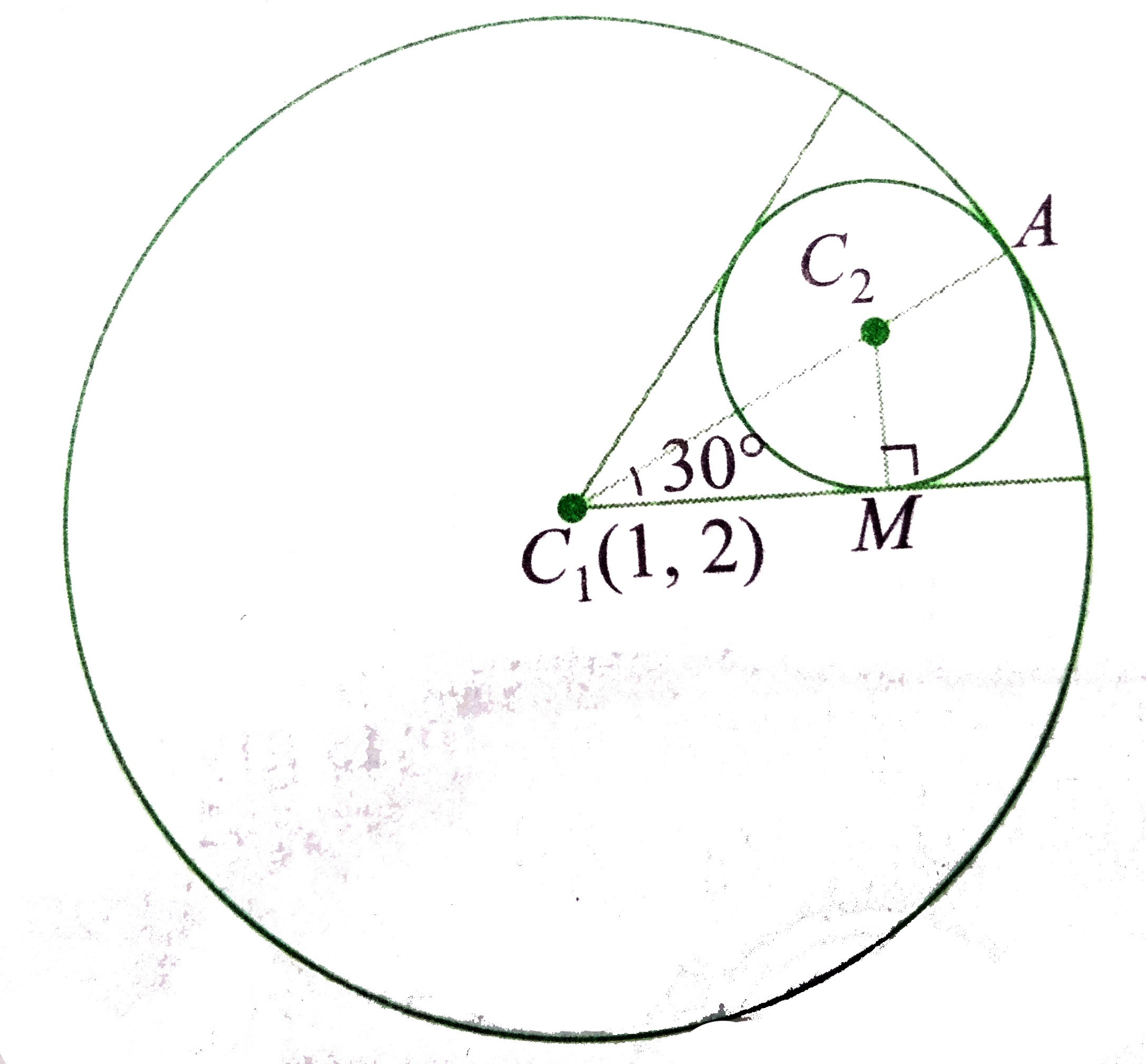
Given circle is `x^(2)+y^(2)-4y-2x-4=0`
Centre is `C_(1)(1,2)` and radius is `r_(1)=sqrt((-2)^(2)+(-1)^(2)-(-4))=3`.
Let the centre of the variable circles touching given circle be `C_(2)(h,k)`.
Angle between tangents drawn from `C_(1)(1,2)` to variable circle is `60^(@)`.
In triangle `C_(1)MC_(2)`.
`sin 30^(@)=(C_(2)M)/(C_(1)C_(2))`
`implies sin 30^(@)=(C_(2)A)/(C_(1)C_(2))`
`implies (1)/(2)=(C_(1)A-C_(1)C_(2))/(C_(1)C_(2))=(3-C_(1)C_(2))/(C_(1)C_(2))`
`implies C_(1)C_(2)=2`
`implies sqrt((h-1)^(2)+(k-2)^(2))=2`
Therefore, required locus is `(x-1)^(2)+(y-2)^(2)=4`.