Home
Class 12
MATHS
If the circle x^2+y^2+2gx+2fy+c=0 bisect...

If the circle `x^2+y^2+2gx+2fy+c=0` bisects the circumference of the circle `x^2+y^2+2g^(prime)x+2f^(prime)y+c^(prime)=0` then prove that `2g^(prime)(g-g^(prime))+2f^(prime)(f-f^(prime))=c-c '`

Text Solution

Verified by Experts

Given circels are
`S_(2)-=x^(2)+y^(2)+2gx+2fy+c=0` (1)
`S_(2)-= x^(2)+y^(2)+2g'x+2f'y+c'=0` (2)
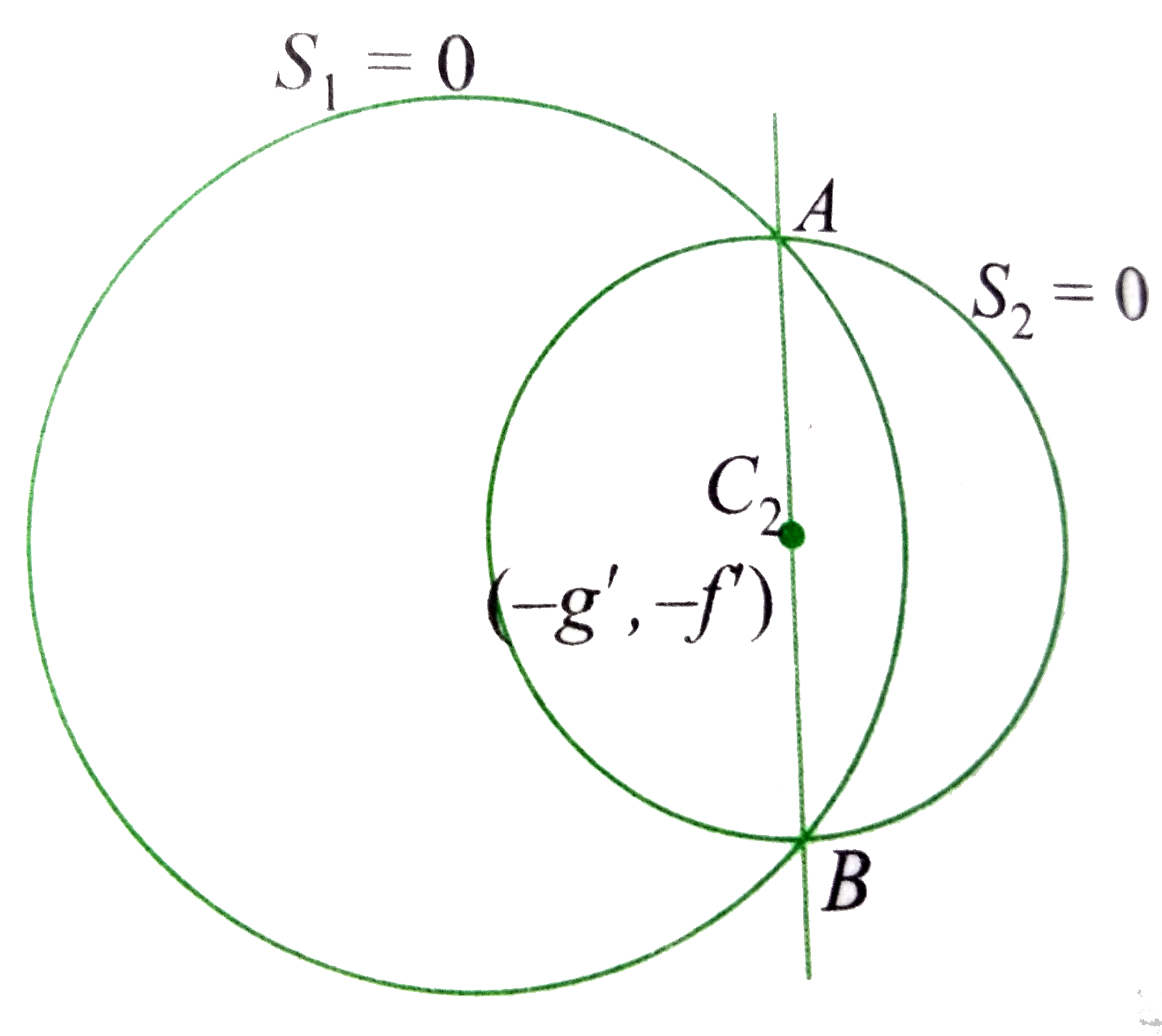
It is given that circle `S_(1)=0` bisects the circumference of the circle `S_(2)=0`. So, the common chord of circles paseses through the centre of the circle `S_(2)=0`.
Equation of common chord of the circles is `2x(g-g')+2y(f-f')+c-c'=0`.
This chord passes through the centre `( -g',-f')` of second circle.

`:. -2g'(g-g')-2f'(f-f')+c-c'=0`
`implies 2g'(g-g')+2f'(f-f')=c-c'`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    CENGAGE PUBLICATION|Exercise Examples|13 Videos

  • CIRCLE

    CENGAGE PUBLICATION|Exercise CONCEPT APPLICATION EXERCISE 4.1|1 Videos

  • BINOMIAL THEOREM

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

Similar Questions

Explore conceptually related problems

If f(x)=x|x|, then prove that f^(prime)(x)=2|x|

The condition that one of the straight lines given by the equation a x^2+2h x y+b y^2=0 may coincide with one of those given by the equation a^(prime)x^2+2h^(prime)x y+b^(prime)y^2=0 is (a b^(prime)-a^(prime)b)^2=4(h a^(prime)-h^(prime)a)(b h^(prime)-b^(prime)h) (a b^(prime)-a^(prime)b)^2=(h a^(prime)-h^(prime)a)(b h^(prime)-b^(prime)h) (h a^(prime)-h^(prime)a)^2=4(a b^(prime)-a^(prime)b)(b h^(prime)-b^(prime)h) (b h^(prime)-b^(prime)h)^2=4(a b^(prime)-a^(prime)b)(h a^(prime)-h^(prime)a)

The line A x+B y+C=0 cuts the circle x^2+y^2+a x+b y+c=0 at Pa n dQ . The line A^(prime)x+B^(prime)x+C^(prime)=0 cuts the circle x^2+y^2+a^(prime)x+b^(prime)y+c^(prime)=0 at Ra n dSdot If P ,Q ,R , and S are concyclic, then show that |a-a ' b-b ' c-c ' A B C A ' B ' C '|=0

If (a x^2+b x+c)y+(a^(prime)x^2+b^(prime)x+c^(prime))=0 and x is a rational function of y , then prove that (a c^(prime)-a^(prime)c)^2=(a b^(prime)-a^(prime)b)xx(b c^(prime)-b^(prime)c)dot

Statement 1 : If two circles x^2+y^2+2gx+2fy=0 and x^2+y^2+2g^(prime)x+2f^(prime)y=0 touch each other, then f^(prime)g=fg^(prime)dot Statement 2 : Two circles touch other if the line joining their centers is perpendicular to all possible common tangents.

If the equations x^2+p x+q=0 and x^2+p^(prime)x+q^(prime)=0 have a common root, then it must be equal to a. (p^(prime)-p ^(prime) q)/(q-q^(prime)) b. (q-q ')/(p^(prime)-p) c. (p^(prime)-p)/(q-q^(prime)) d. (p q^(prime)-p^(prime) q)/(p-p^(prime))

If the circles x ^(2) +y^(2) +2gx +2fy =0 and x ^(2) +y^(2) +2g'x+ 2f'y=0 touch each other then-

If the quadrilateral formed by the lines a x+b y+c=0,a^(prime)x+b^(prime)y+c=0,a x+b y+c^(prime)=0,a^(prime)x+b^(prime)y+c^(prime) =0 has perpendicular diagonals, then (a) b^2+c^2=b^('2)+c^('2) (b) c^2+a^2=c^('2)+a^('2) (c) a^2+b^2=a^('2)+b^('2) (d) none of these

If f(x),g(x) and h(x) are three polynomials of degree 2, then prove that phi(x) = |[f(x),g(x),h(x)],[f ^ (prime)(x),g^(prime)(x),h^(prime)(x)],[f^(primeprime)(x),g^(primeprime)(x),h^(primeprime)(x)]| is a constant polynomial.

Suppose that f(x) is a quadratic expresson positive for all real x If g(x)=f(x)+f^(prime)(x)+f^(prime prime)(x), then for any real x (where f^(prime)(x) and f^(primeprime)(x) represent 1st and 2nd derivative, respectively). (a) g(x) 0 (c). g(x)=0 (d). g(x)geq0