Home
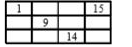
Class 14
MATHS
It is possible to arrange eight of the n...

It is possible to arrange eight of the nine numbers 2, 3, 4, 5, 7, 10, 11, 12, 13 in the vacant squares of the 3 by 4 array shown below so that the arithmetic average of the numbers in each row and column is the same integer.

Which one of the nine numbers must be left out when completing the array ?

A

4

B

5

C

7

D

10

Text Solution

Verified by Experts

The correct Answer is:
D
Promotional Banner

Topper's Solved these Questions

  • PROGRESSIONS

    DISHA PUBLICATION|Exercise EXPERT LEVEL|25 Videos

  • PROGRESSIONS

    DISHA PUBLICATION|Exercise TEST YOURSELF|15 Videos

  • PROGRESSIONS

    DISHA PUBLICATION|Exercise FOUNDATION LEVEL|36 Videos

  • PROFIT, LOSS AND DISCOUNT

    DISHA PUBLICATION|Exercise Test Yourself|15 Videos

  • QUADRATIC AND CUBIC EQUATIONS

    DISHA PUBLICATION|Exercise Test Yourself |15 Videos

Similar Questions

Explore conceptually related problems

It is possible to arrange eight of the nine numbers 2, 3, 4, 5, 7, 10, 11, 12, 13 in the vacant squares of the 3 by 4 array shown below so that the arithmetic average of the numbers in each row and column is the same integer. The arithmetic average is

The numbers 2 3 4 5 6 7 8 are to be placed one per square in the diagram as shown below such that the sum of the four numbers in the horizontal row as well as vertical row is 21 then the number of ways in which this can be done is ?

Cosider the number 1,2,3,4,5,6,7,8,9 and 10.If 1 is added to each number the variance of the number so obtained is

EXAMPLE 3 A magic square is an array of numbers having the same number of rows and columns and the sum of the numbers in a row column and the sum of the numbers in each row column or diagonal being the same.Fill in the blank cells of the following magic square.

Nine numbers 1,2,3.........9 are put into a 3times3 array, so that each number occur exactly once. Find the probability that the sum of the numbers in atleast one horizontal row is greater than 21.

What number must be added to each of the numbers 7,11 and 19 so that the resulting numbers may be in continued proportion? 3 b.-3 c.4 d.-4

In each of the following questions, two rows of numbers are given. The resultant number in each row is to be worked out separately based on the following rules and the questions below the rows of numbers are to be answered. The operations of numbers progress from the left to the right. Rules: (i) If an odd number is followed by another composite odd number, they are to be multiplied (ii) If an even number is followed by an odd number, they are to be added. (iii) If an even number is followed by a number which is the perfect square, the even number is to be subtracted from the perfect square. (iv) If an odd number is followed by an even number, the first number is to be subtracted from the first one. (v) If an odd number is followed by an prime odd number, the first number is to be divided by the second number. 67 12 11 20 x 11 Which of the following will be the answer if the resultant of the two rows are added ? 1) 45 2) 54 3) 36 4) 18 5) None of these

In each of the following questions, two rows of numbers are given. The resultant number in each row is to be worked out separately based on the following rules and the questions below the rows of numbers are to be answered. The operations of numbers progress from the left to the right. Rules: (i) if a two-digit odd number is followed by a prime number. (ii) If an even number is followed by another even number, the first number is to be divided by the second number. (iii) If an odd number is followed by a composite odd number, the first number is to be added to the second number . (iv) If an even number which is multiple of 5 is followed by another number which is a multiple of 5, the second number is to be subtracted from the first number. (v) If a number which is perfect square , the resultant number is the product of the square roots of the two numbers. 50 15 27 15 5 7 What is the sum of the resultants of the two rows ? 1) 62 2) 630 3) 587 4) 392 5) None of these

DISHA PUBLICATION-PROGRESSIONS-STANDARD LEVEL
  1. The sum of thirty-two consecutive natural numbers is a perfect square....

    Text Solution

    |

  2. If a, b and c are in HP, then (a)/(b+c), (b)/(c+a) , (c )/(a+b) are in...

    Text Solution

    |

  3. The middle term of arithmetic series 3, 7, 11...147, is

    Text Solution

    |

  4. If a man saves 4 more each year than he did the year before and if he ...

    Text Solution

    |

  5. What is the maximum sum of the terms in the arithmetic progression 25 ...

    Text Solution

    |

  6. (1-1/n) + (1 - 2/n) + (1 - 3/n)+ …… upto n terms = ?

    Text Solution

    |

  7. IF 1^3+2^3+…….+9^3=2025 then the value of (0.11)^3 +(0.22)^3+……+(0.99)...

    Text Solution

    |

  8. How many terms are identical in the two APs 1,3, 5,... up to 120 terms...

    Text Solution

    |

  9. If the sum of the first 2n terms of the AP 2, 5, 8 ....is equal to the...

    Text Solution

    |

  10. It is possible to arrange eight of the nine numbers 2, 3, 4, 5, 7, 10,...

    Text Solution

    |

  11. It is possible to arrange eight of the nine numbers 2, 3, 4, 5, 7, 10,...

    Text Solution

    |

  12. Seven integers A, B, C, D, E, F and G are to be arranged in an increas...

    Text Solution

    |

  13. Seven integers A, B, C, D, E, F and G are to be arranged in an increas...

    Text Solution

    |

  14. Seven integers A, B, C, D, E, F and G are to be arranged in an increas...

    Text Solution

    |

  15. Seven integers A, B, C, D, E, F and G are to be arranged in an increas...

    Text Solution

    |

  16. If the positive real numbers a, b and c are in Arithmetic Progression,...

    Text Solution

    |

  17. After striking a floor a rubber ball rebounds (7/8)th of the height fr...

    Text Solution

    |

  18. The sum of (1/2 . 2/2)/(1^3) + (2/2 . 3/2)/(1^3 + 2^3) + (3/2 . 4/2)...

    Text Solution

    |

  19. The sum of the first three terms of the arithmetic progression is 30 a...

    Text Solution

    |

  20. The sum of an infinite GP is 162 and the sum of its first n terms is 1...

    Text Solution

    |