Home
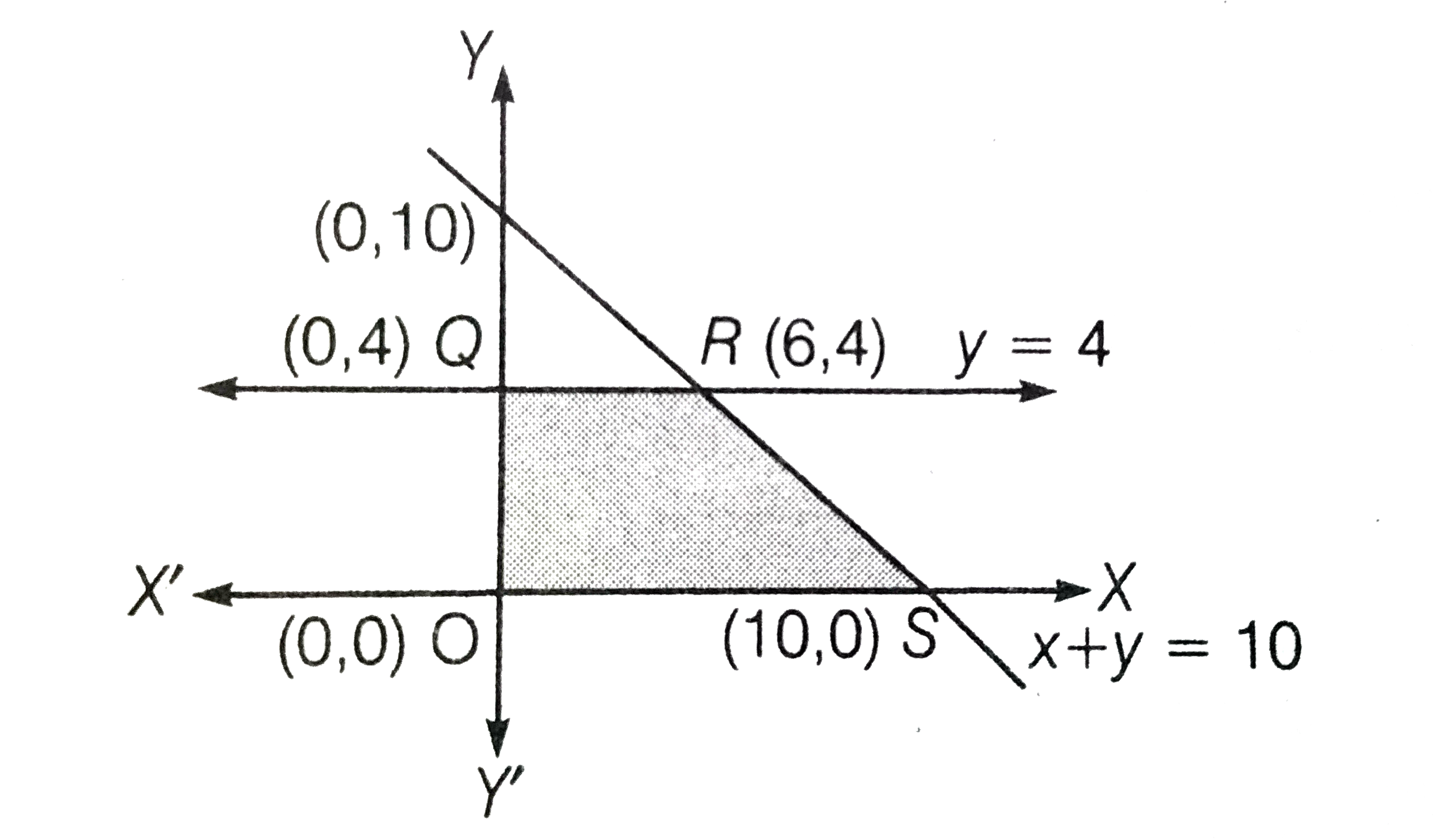
Class 12
MATHS
The minimum value of Z = 5x - 4y subject...

The minimum value of Z = 5x - 4y subject to constraints ` x+y le 10 , y le 4, x,y gt 0 ` will be at the point

A

(10,4)

B

(-10,4)

C

(6,4)

D

(0,4)

Text Solution

Verified by Experts

The correct Answer is:
D
Here, QRSOQ is the feasible region

`"Given , " "Z=5x -4y `
`"At Q(0,4), " "Z= -16 (minmum) `
`"At R (6,4), " "Z=14 `
`"At O(0,0), " "Z=0 `
`"At S(10,0), , " "Z=50 `
`therefore ` Minimum value of Z is - 16 which is attained at point (0,4)
Promotional Banner

Topper's Solved these Questions

  • Linear Programming

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise EXERCISE 2 (MISCELLANEOUS PROBLEMS )|30 Videos

  • Linear Programming

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|13 Videos

  • Linear Programming

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|13 Videos

  • LINE

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET Corner|3 Videos

  • MATHEMATICAL LOGIC

    MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS|Exercise MHT CET CORNER|22 Videos

Similar Questions

Explore conceptually related problems

The minimum value of P = 6x + 16y subject to constraints x le 40 , y le 20 and x , y ge 0 is

The maximum value of Z = 3x + 4y subject to the constraints: x + y le 4, x ge 0, y ge 0 is :

The minimum value of Z= 4x+5y subject to the constraints x le 30, yle 40 and x ge 0,y ge 0 is

The maximum value of Z = 4x + 2y subject to the constraints 2x+3y le 18,x+y ge 10, x , y ge 0 is

Maximum value of Z = 3x + 4y subject to the constraints x + y le 4, x ge 0, y ge 0 is 16.

The maximum value of z = 10x + 6y subject to constraints x ge 0, y ge 0, x +y le 12, 2x +y le 20 is