Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-GRAVITATION-Solved Examples
- Three particles, each of the mass m are situated at the vertices of an...
Text Solution
|
- In the above problem, find total mechanical energy of the system .
Text Solution
|
- Two concentric shells of masses M(1) and M(2) are concentric as shown....
Text Solution
|
- Gravitational potential energy between two points masses is U = -(Km...
Text Solution
|
- Imagine a light planet revolving around a very massive star in a circu...
Text Solution
|
- There is a smooth tunnel upto centre C of a solid sphere of mass 'M' a...
Text Solution
|
- A particle of mass 'm' is projected from the surface of earth with vel...
Text Solution
|
- In the figure shown in text, m(1) = m, m(2) = 2m and initial distance ...
Text Solution
|
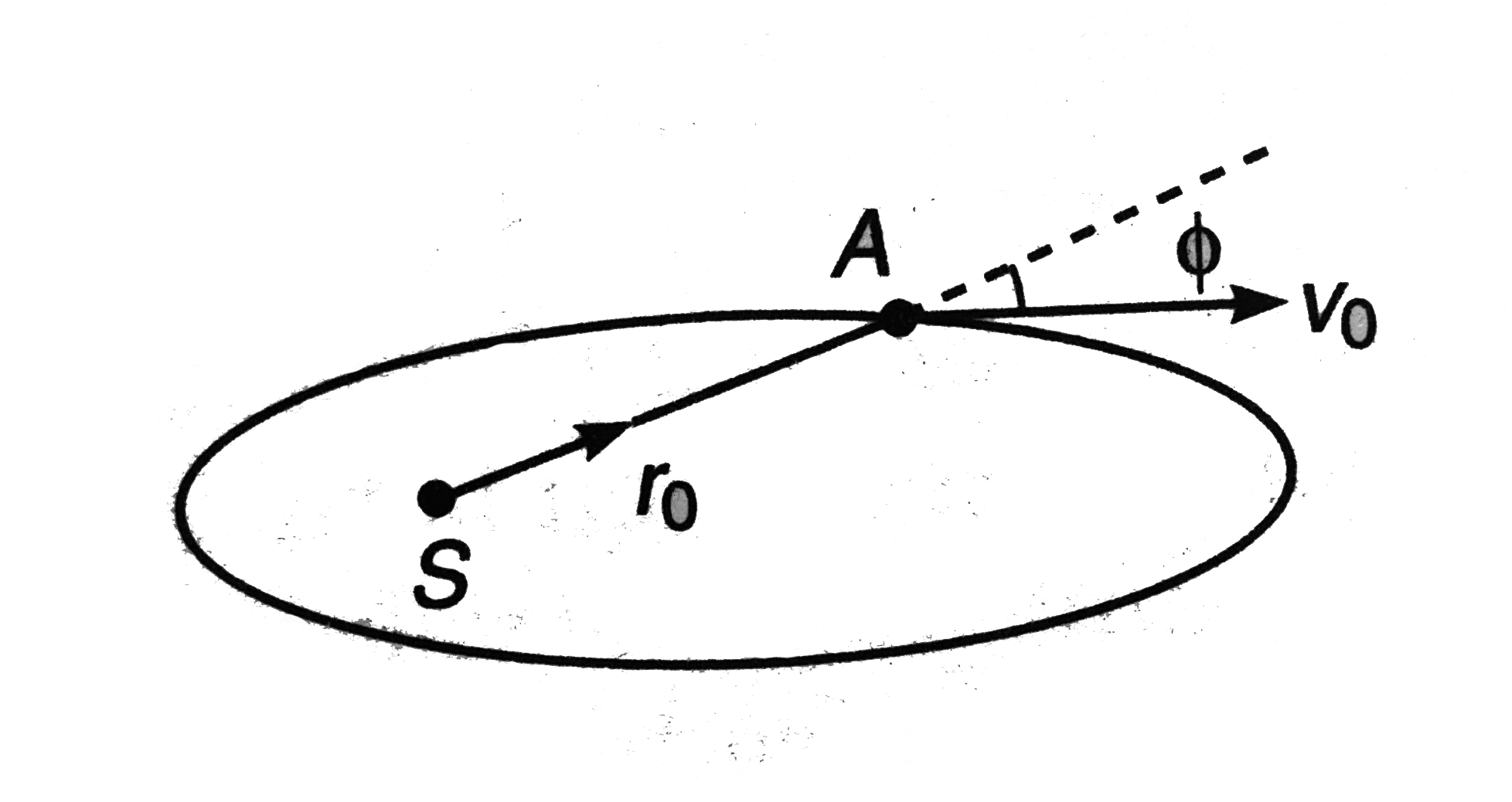
- Find the maximum and minimum distances of the planet A from the sun S...
Text Solution
|
- A projectile of mass m is fired from the surface of the earth at an an...
Text Solution
|
- A plant of mass m(1) revolves round the sun of mass m(2). The distance...
Text Solution
|
- In the problem discussed in the text, find E - r expressions for insid...
Text Solution
|
- Two points masses 'm' and 2m are kept at certain distance as shows in ...
Text Solution
|
- In the problem discussed in the text, find the values of E and V at p ...
Text Solution
|
- Distance between the centres of two stars is 10a. The masses of these ...
Text Solution
|
- Three spherical shells of masses M, 2M and 3M have radii R, 3R and 4R ...
Text Solution
|