Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY-GRAVITATION-Miscellaneous Examples
- Explain the reason of weightlessness inside a satellite.
Text Solution
|
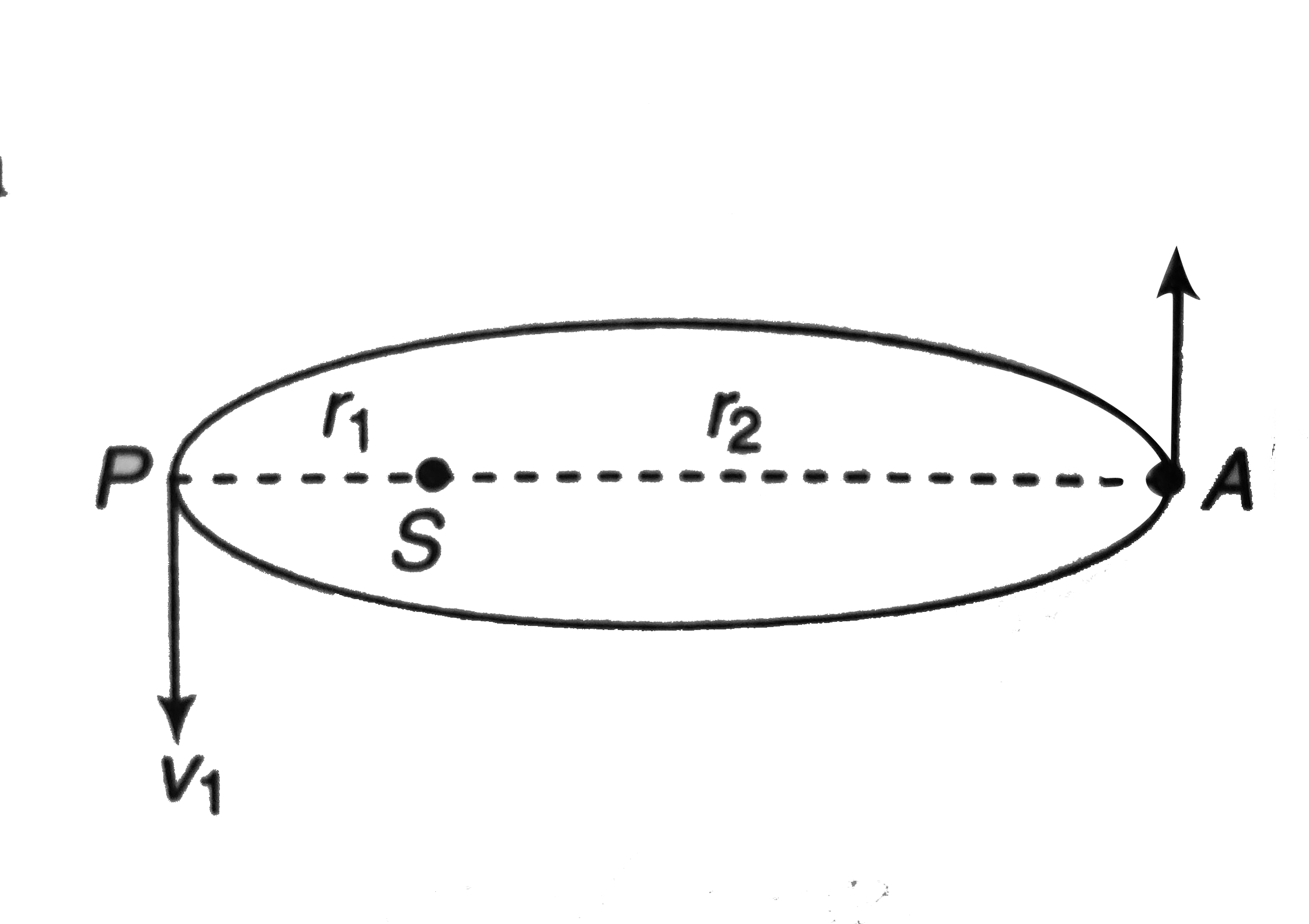
- Find the speeds of a planet of mass m in its perihelion and aphelion p...
Text Solution
|
- The minimum and maximum distances of a satellite from the center of th...
Text Solution
|
- A planet of mass m revolves in elliptical orbit around the sun of mass...
Text Solution
|
- If a planet was suddenly stopped in its orbit supposed to be circular,...
Text Solution
|
- A satellite is revolving round the earth in a circular orbit of radius...
Text Solution
|
- An earth satellite is revolving in a circular orbit of radius a with v...
Text Solution
|
- Binary stars of comparable masses m(1) and m(2) rotate under the influ...
Text Solution
|