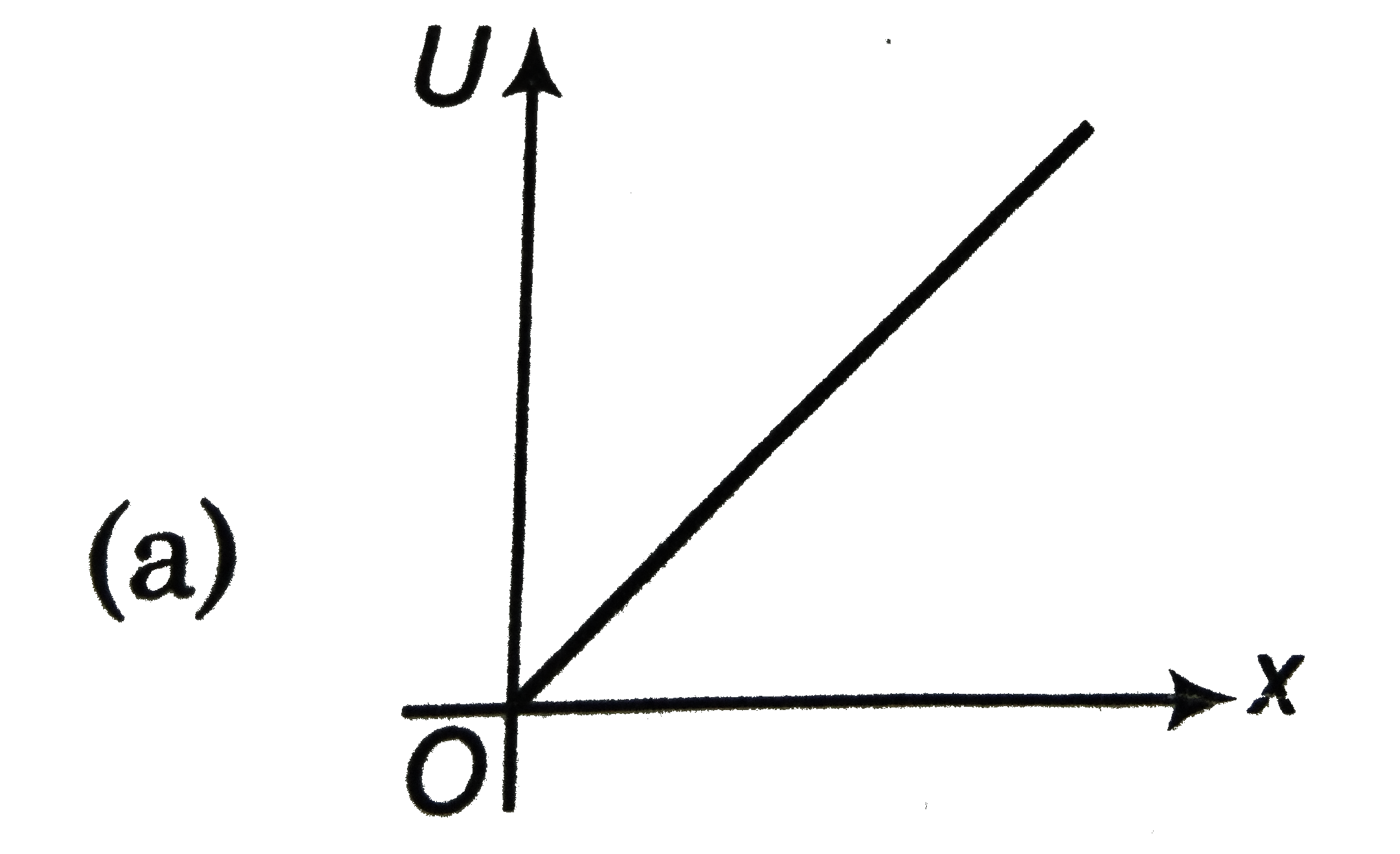
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY|Exercise Level 1 Subjective|39 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Level 2 Single Correct|28 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Level 1 Assertion And Reason|10 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY|Exercise More than One Option is Correct|3 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-SIMPLE HARMONIC MOTION-Level 1 Single Correct
- Two simple harmonic motions are given by y(1) = a sin [((pi)/(2))t + p...
Text Solution
|
- A particle starts performing simple harmonic motion. Its amplitude is ...
Text Solution
|
- Which of the following is not simple harmonic function ?
Text Solution
|
- The disperod of a particle varies according to the relation x=4 (cos p...
Text Solution
|
- Two pendulums X and Y of time periods 4 s and 4.2s are made to vibrate...
Text Solution
|
- A mass M is suspended from a massless spring. An additional mass m str...
Text Solution
|
- Two bodies P and Q of equal masses are suspended from two separate mas...
Text Solution
|
- A disc of radius R is pivoted at its rim. The period for small oscilla...
Text Solution
|
- Identify the correct variation of potential energy U as a function of ...
Text Solution
|
- If the length of a simple pendulum is equal to the radius of the earth...
Text Solution
|
- The displacement - time (x - t) graph of a particle executing simple h...
Text Solution
|
- In the figure shown the time period and the amplitude respectively, wh...
Text Solution
|
- The equation of motion of a particle of mass 1g is (d^(2)x)/(dt^(2)) +...
Text Solution
|
- The spring as shown in figure is kept in a stretched position with ext...
Text Solution
|
- The mass and diameter of a planet are twice those of earth. What will ...
Text Solution
|
- The resultant amplitude due to superposition of three simple harmonic ...
Text Solution
|
- Two SHMs s(1) = a sin omega t and s(2) = b sin omega t are superimpose...
Text Solution
|
- The amplitude of a particle executing SHM about O is 10 cm. Then
Text Solution
|
- A particle is attached to a vertical spring and is pulled down a dista...
Text Solution
|
- A block of mass 1kg is kept on smooth floor of a truck. One end of a s...
Text Solution
|