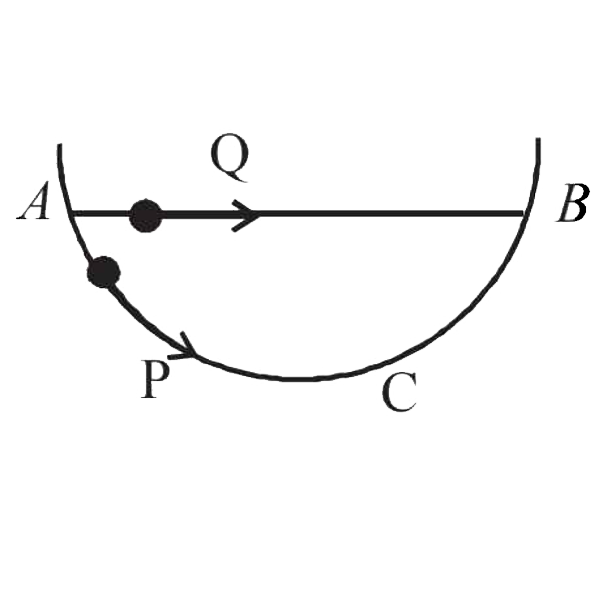
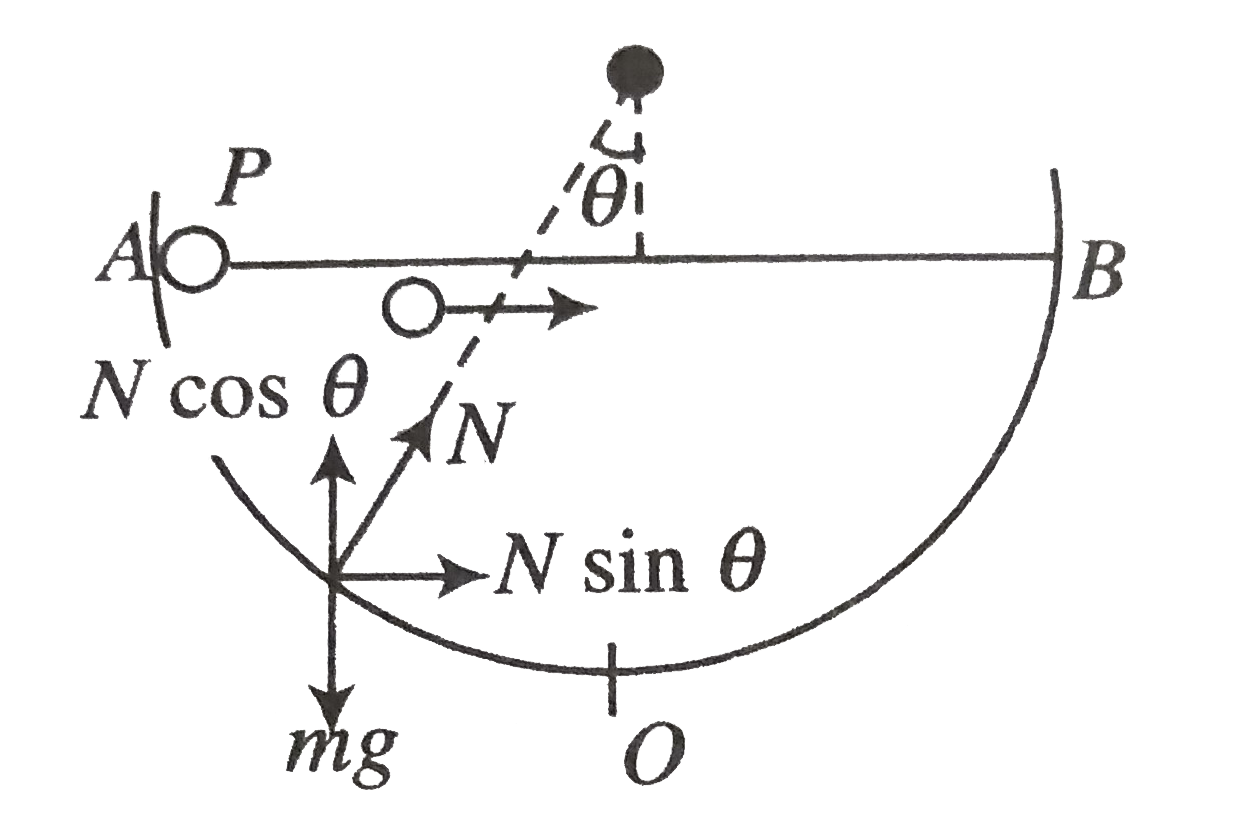
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
NEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Assertion -reasoning|2 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Integer type|1 VideosNEWTON'S LAWS OF MOTION 2
CENGAGE PHYSICS|Exercise Single correct answer type|13 VideosNEWTON'S LAWS OF MOTION 1
CENGAGE PHYSICS|Exercise Integer|5 VideosPROPERTIES OF SOLIDS AND FLUIDS
CENGAGE PHYSICS|Exercise INTEGER_TYPE|2 Videos
Similar Questions
Explore conceptually related problems