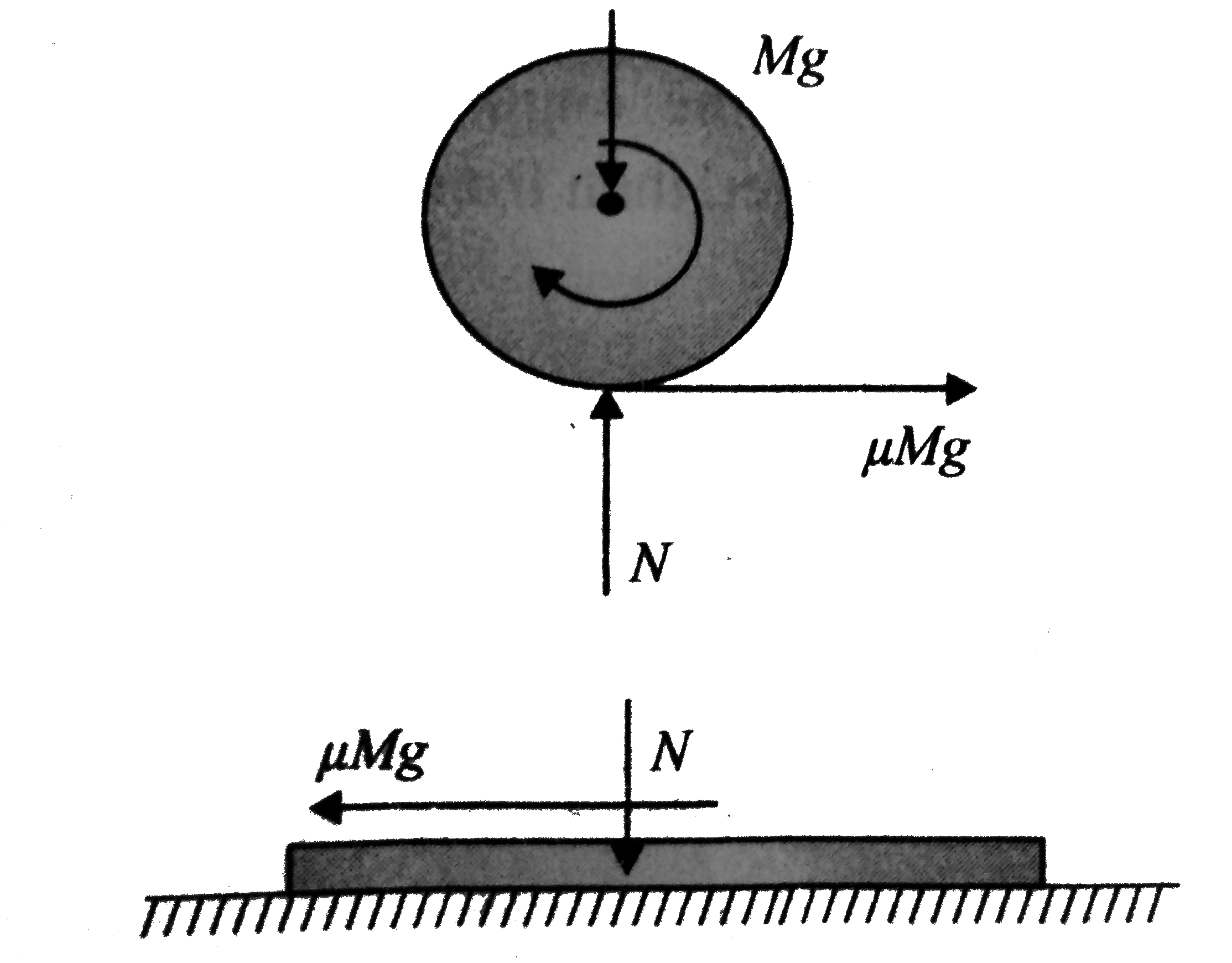
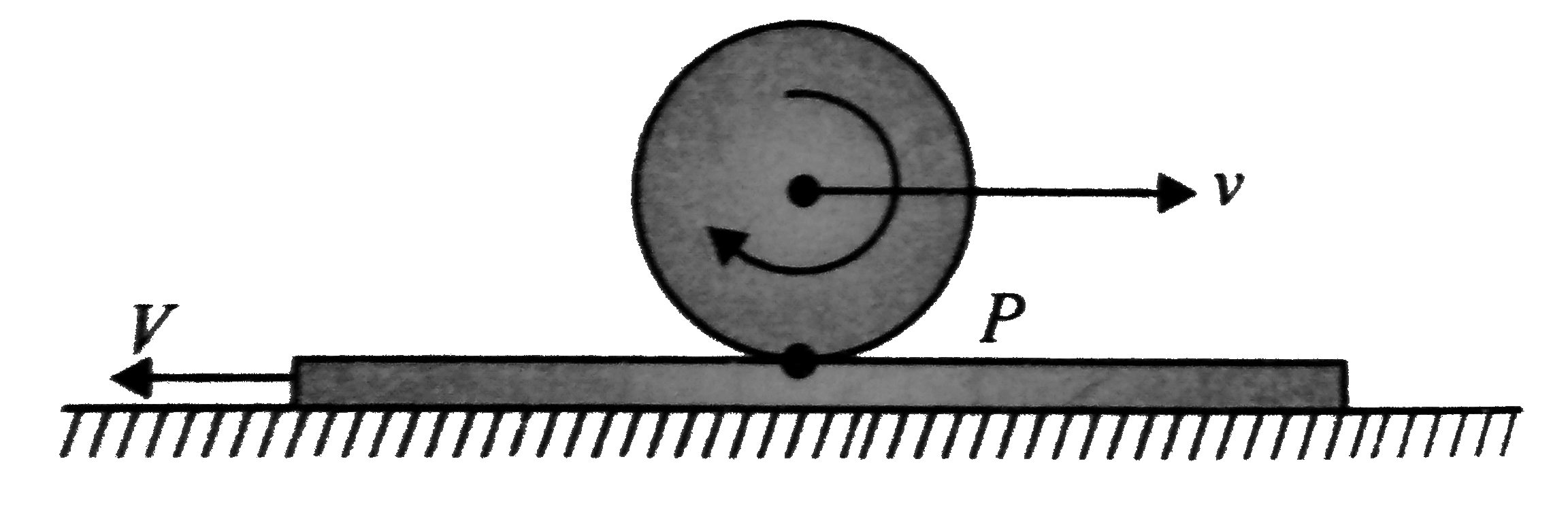
Text Solution
Verified by Experts
Topper's Solved these Questions
RIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Exercise 3.4|13 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Subjective|19 VideosRIGID BODY DYNAMICS 2
CENGAGE PHYSICS|Exercise Exercise 3.2|13 VideosRIGID BODY DYNAMICS 1
CENGAGE PHYSICS|Exercise Integer|11 VideosSOUND WAVES AND DOPPLER EFFECT
CENGAGE PHYSICS|Exercise Integer|16 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Exercise 3.3
- A sphere moving with a velocity v(0) on a smooth surface suddenly ente...
Text Solution
|
- A cylinder of mass at and radius R rolls on a stationary plank of mass...
Text Solution
|
- Calculate the kinetic energy of a tractor crawler belt of mass m if th...
Text Solution
|
- A constant horizontal force of 10 N is applied at the centre of a whee...
Text Solution
|
- A uniform solid cylinder of mass m rests on two horizontal planks. A t...
Text Solution
|
- A load of mass m is attached to the end of a string wound on a cylinde...
Text Solution
|
- Find the tension in the tape and the linear acceleration of the cylind...
Text Solution
|
- A spool (consider it as a double disc system joined by a short tube at...
Text Solution
|
- A solid cylinder wheel of mass M and radius R is pulled by a force F a...
Text Solution
|
- Find the acceleration of a system consisting of a cylinder of mass m a...
Text Solution
|
- A uniform solid cylinder of mass m rests on two horizontal planks as s...
Text Solution
|
- A bullet of mass m moving with a velocity of u just grazes the top of ...
Text Solution
|
- A small solid marble of mass M and radius r rolls down along the loop ...
Text Solution
|
- A solid sphere of mass M is placed on the top of a plank of the same m...
Text Solution
|
- A ball of mass m is released from rest from a height H along a smooth,...
Text Solution
|
- A sphere of mass m and radius R rolls without sliding on a horizontal ...
Text Solution
|
- Find the acceleration of the body if a force F=8 N pulls the string at...
Text Solution
|
- A cotton reel rolls without sliding such that the point P of the strin...
Text Solution
|
- A cotton reel rolls without sliding such that the point P of the strin...
Text Solution
|
- A uniform solid sphere rolls down a vertical surface without sliding. ...
Text Solution
|