Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTRIC POTENTIAL
CENGAGE PHYSICS|Exercise Exercise 3.3|9 VideosELECTRIC POTENTIAL
CENGAGE PHYSICS|Exercise Subjective|28 VideosELECTRIC POTENTIAL
CENGAGE PHYSICS|Exercise Exercise 3.1|23 VideosELECTRIC FLUX AND GAUSS LAW
CENGAGE PHYSICS|Exercise MCQ s|38 VideosELECTRICAL MEASURING INSTRUMENTS
CENGAGE PHYSICS|Exercise M.C.Q|2 Videos
Similar Questions
Explore conceptually related problems
CENGAGE PHYSICS-ELECTRIC POTENTIAL-Exercise 3.2
- A particle of mass 1 kg and charge 1//3 mu C is projected toward a non...
Text Solution
|
- A cone made of insulating material has a total charge Q spread uniform...
Text Solution
|
- A simple pendulum of length l and bob mass m is hanging in front of a ...
Text Solution
|
- An insulating rod having linear charge density lambda = 40.0 mu Cm^-1 ...
Text Solution
|
- Three concentric spherical conductors of radii a, 2a, and 3a have char...
Text Solution
|
- In the previous problem, if we connect the conductors 1 and 2, 2 and 3...
Text Solution
|
- As shown in, two large parallel vertical conducting plates separated b...
Text Solution
|
- Electrically charged drops of mercury fall from an altitude h into a s...
Text Solution
|
- A small sphere of mass m = 0.5 kg carrying a positive charge q = 110 m...
Text Solution
|
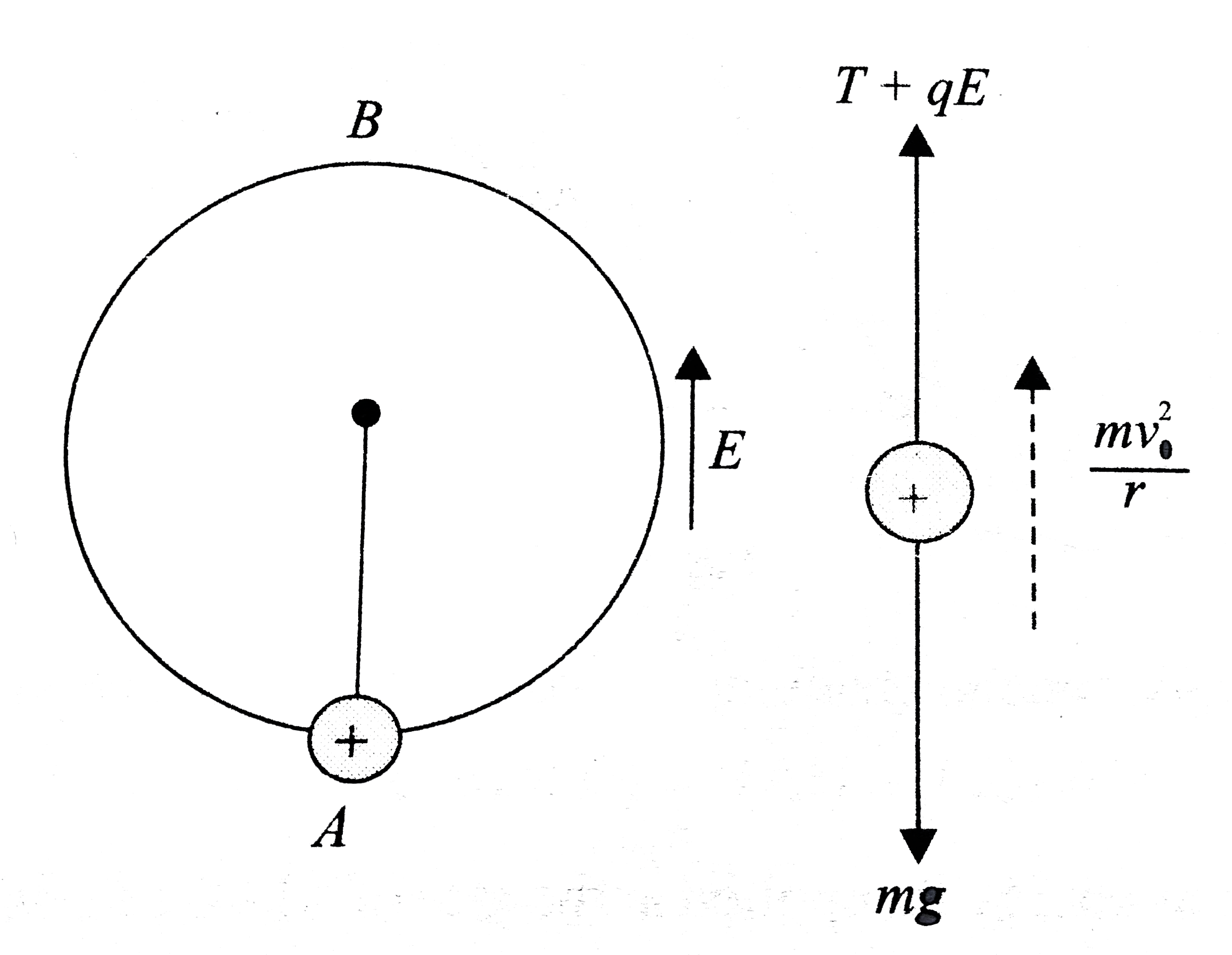 .
.