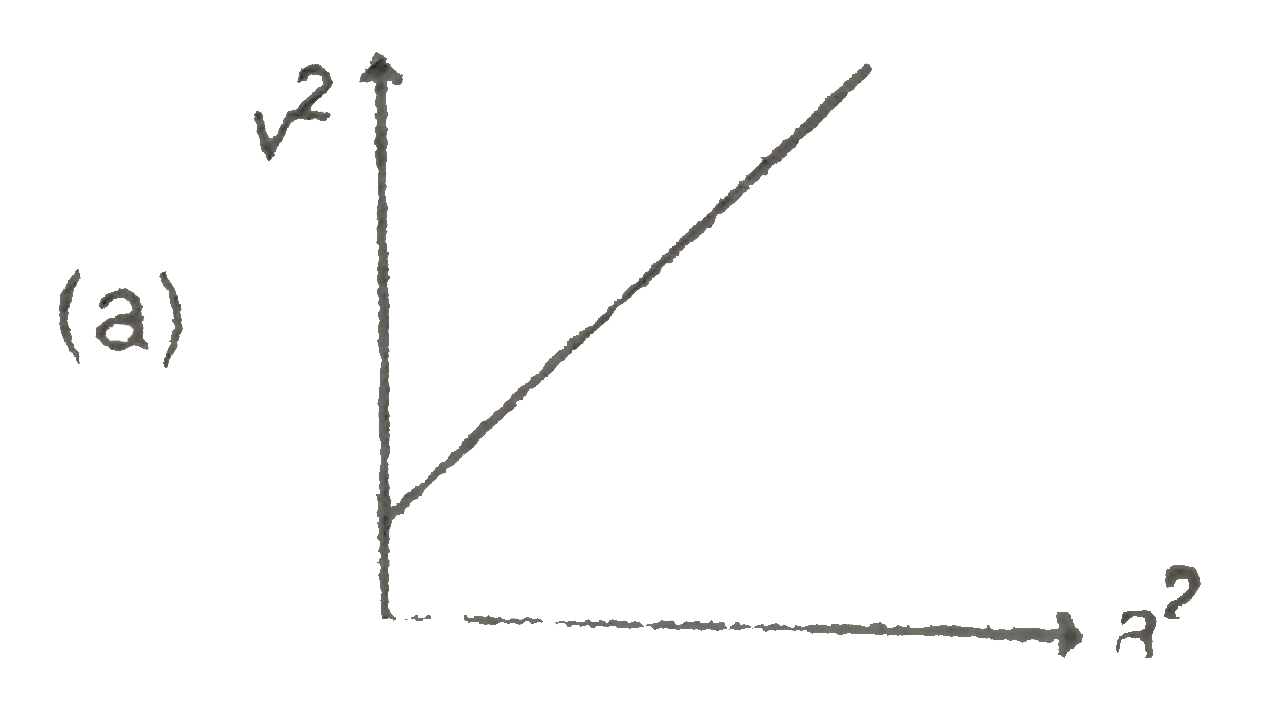
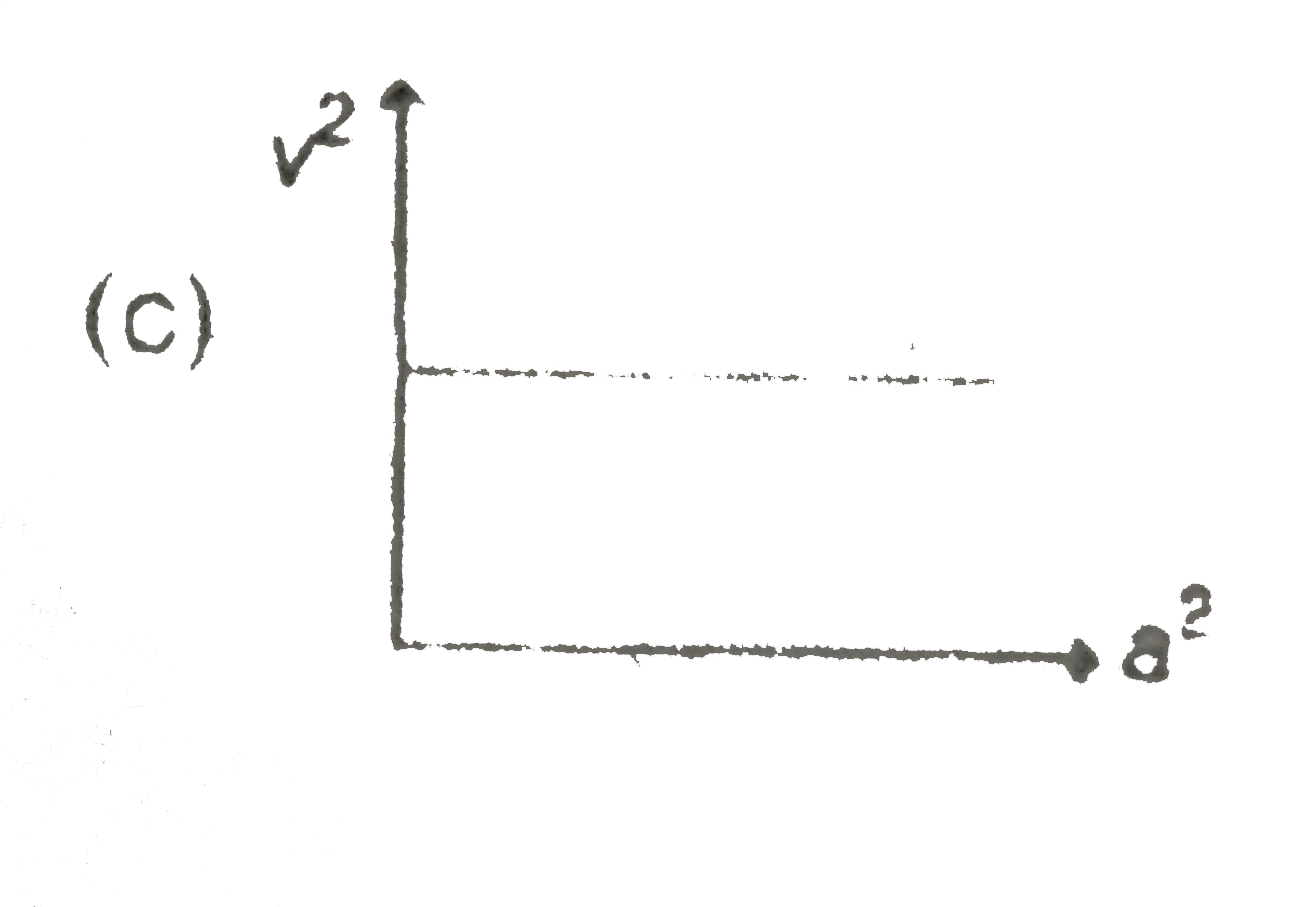
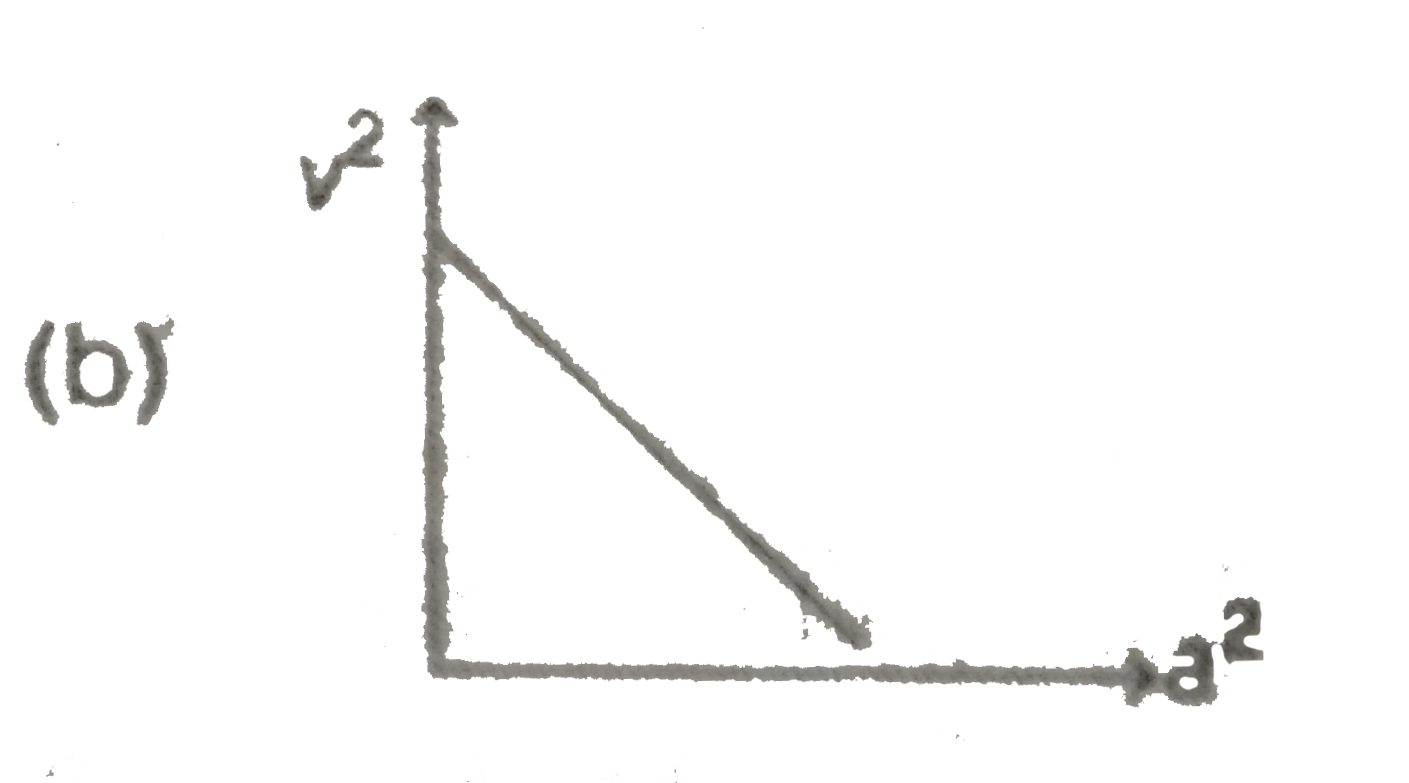A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
SIMPLE HARMONIC MOTION
DC PANDEY|Exercise More than one option is correct|50 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Comprehension types|18 VideosSIMPLE HARMONIC MOTION
DC PANDEY|Exercise Only one question is correct|48 VideosSEMICONDUCTORS AND ELECTRONIC DEVICES
DC PANDEY|Exercise More than One Option is Correct|3 VideosSOLVD PAPERS 2017 NEET, AIIMS & JIPMER
DC PANDEY|Exercise Solved paper 2018(JIPMER)|38 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY-SIMPLE HARMONIC MOTION-JEE Advanced
- Maximum speed of a particle in simple harmonic motion is v(max). Then ...
Text Solution
|
- Two particles execute simple harmonic motion of the same amplitude and...
Text Solution
|
- A block is kept on a rough horizontal plank. The coefficient of fricti...
Text Solution
|
- A particle of mass m is executing osciallations about the origin on th...
Text Solution
|
- A ball of mass m when dropped from certain height as shown in diagram,...
Text Solution
|
- A particle performs SHM in a straight line. In the first second, start...
Text Solution
|
- The angular frequency of a spring block system is omega(0). This syste...
Text Solution
|
- A small ball of density rho id released from rest from the surface of ...
Text Solution
|
- A constant force produces maximum velocity V on the block connected to...
Text Solution
|
- Two blocks of masses m(1)=1kg and m(2) = 2kg are connected by a spring...
Text Solution
|
- U.r graph of a particle performing SHM is as shown in figure. What con...
Text Solution
|
- Two particles are in SHM along same line with same amplitude A and sam...
Text Solution
|
- A plank of area of cross-section A is half immersed in liquid 1 of den...
Text Solution
|
- A mass M is performing linear simple harmonic motion. Then correct gra...
Text Solution
|
- A test tube of length l and area of cross-section A has some iron fill...
Text Solution
|
- A particle is executing SHM according to the equation x=A cosomegat. A...
Text Solution
|
- A particle performs SHM of amplitude A along a straight line .When it ...
Text Solution
|
- In the figure, a block of mass m is rigidly attached to two identical ...
Text Solution
|
- A particle is placed at the lowest point of a smooth wire frame in the...
Text Solution
|
- Two springs, each of spring constant k = 100N/m are attached to a bloc...
Text Solution
|