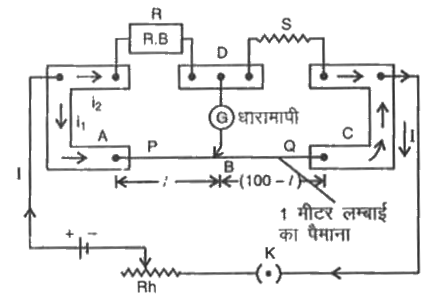
लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
विद्युत परिपथ
MITTAL PUBLICATION|Exercise अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न)|15 Videosविद्युत परिपथ
MITTAL PUBLICATION|Exercise प्रतियोगी परीक्षा संबंधी प्रश्न ( बहुविकल्पीय प्रश्न)|20 Videosविद्युत परिपथ
MITTAL PUBLICATION|Exercise अन्य महत्वपूर्ण प्रश्न (लघु उत्तरीय प्रश्न)|3 Videosविद्युत धारिता
MITTAL PUBLICATION|Exercise प्रतियोगी परीक्षा संबंधी प्रश्न (बहुविकल्पीय प्रश्न )|16 Videosविद्युत विभव
MITTAL PUBLICATION|Exercise प्रतियोगी परीक्षा संबंधी प्रश्न|15 Videos