A manometer tube contains a liquid of density `4xx10^(3) kg m^(-3)`. When connected to a vessel containing a gas, the liquid level in the other arm of the tube is higher by 20 cm. When connected to another sample of enclosed gas, the liquid level in the other arm of the manometer tube falls 8 cm below the liquid level in the first arm. Which of the two samples exerts more pressure and by what amount ?

Explanation

Difference in level of liquids, `h_(1)=20 cm=0.2 m`
Pressure of the gas in the containing, `p_(1)=p_(a)+rhogh_(1)`

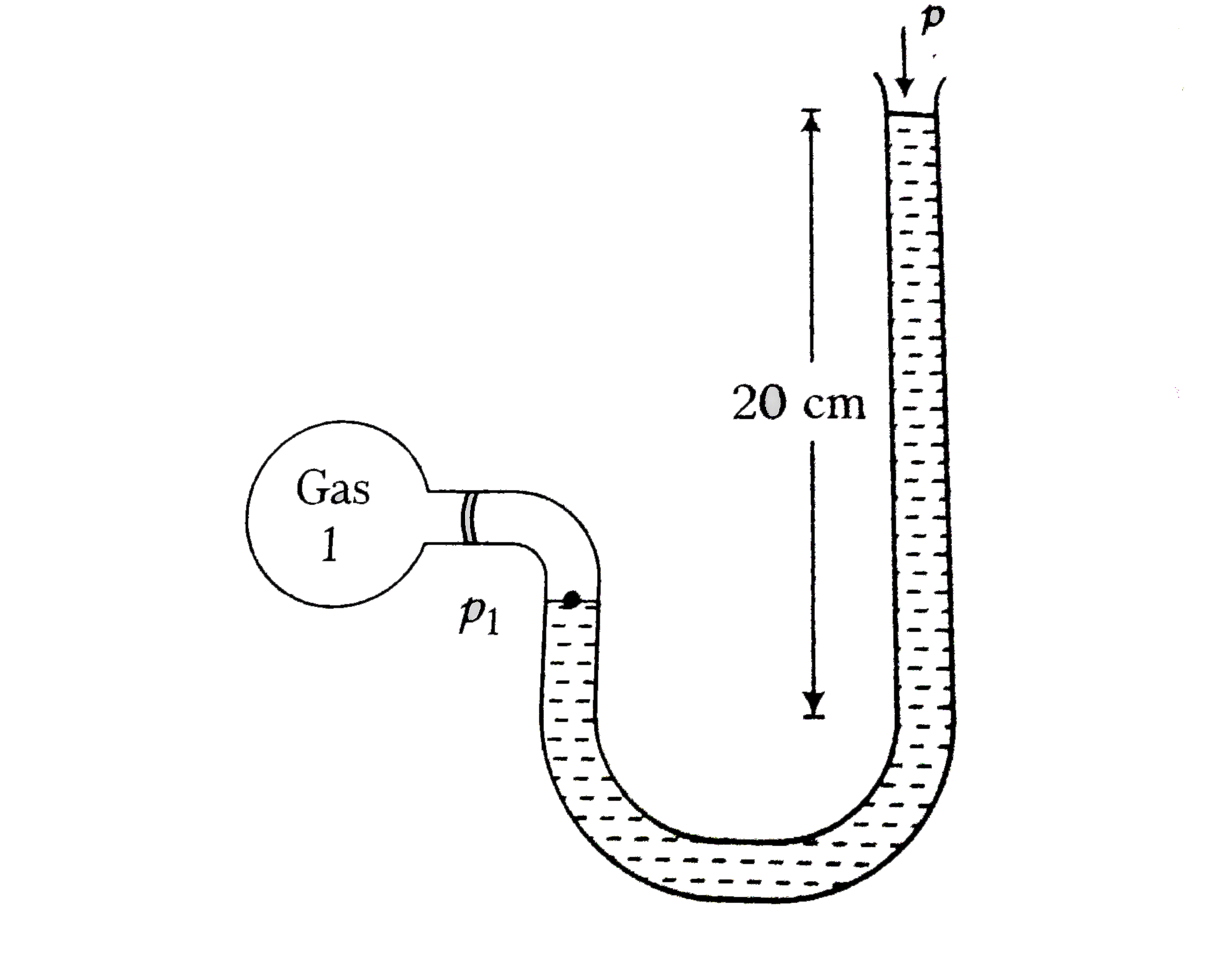
In this case, level of the liquid in the left arm is higher than that in the right arm by 8 cm.
`therefore` Atmospheric pressure `p_(a)` is greater than the pressure exerted by the sample
`implies p_(a)=p_(2)+rho gh_(2) implies p_(2)=p_(a)-rho gh_(2)`
Comparing equations (i) and (ii), it is clear that `p_(1) gt p_(2)`.

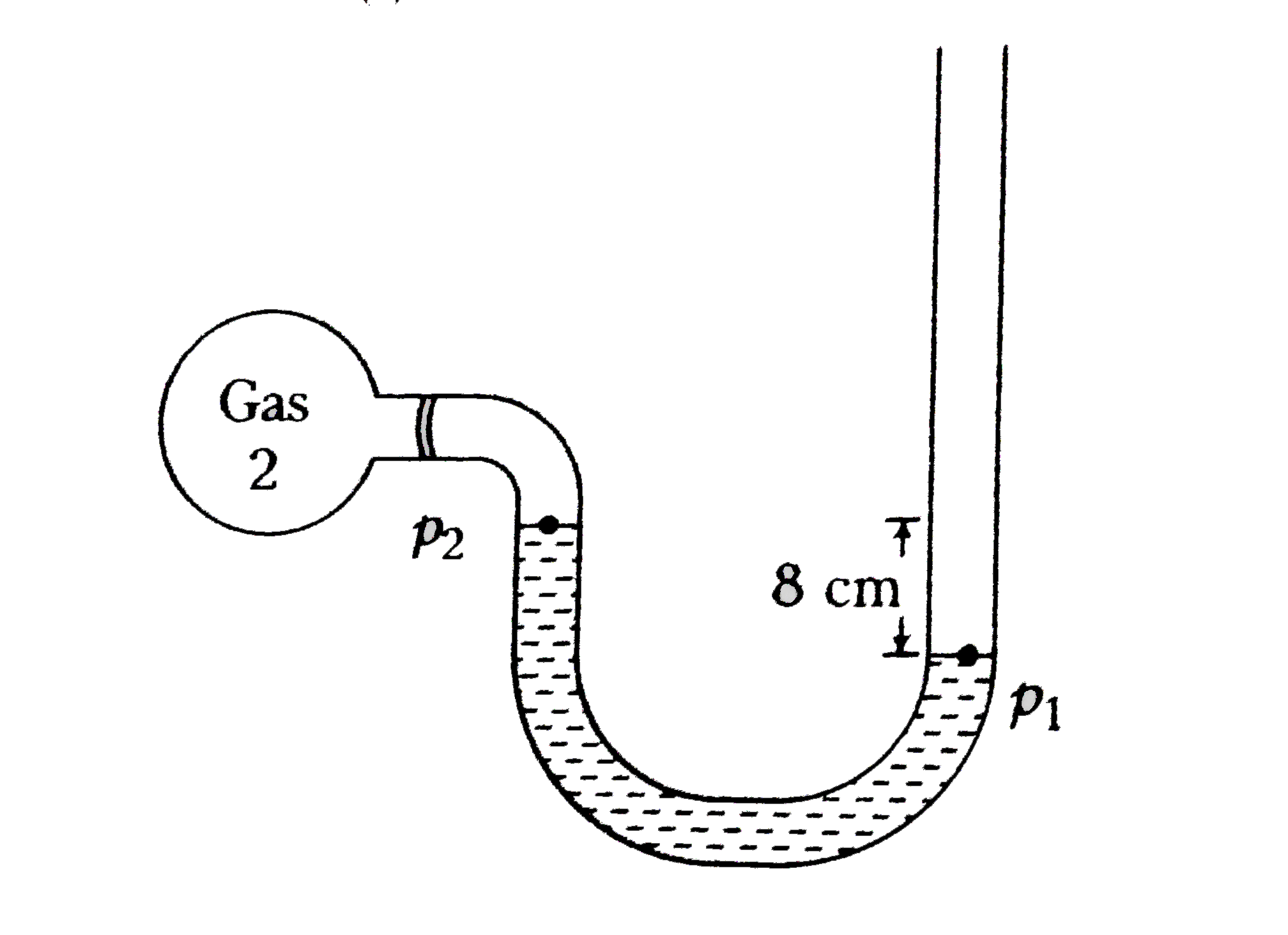
Therefore the gas in sample 1 exerts greater pressure than that in sample 2.
The difference in the two pressures is
`p_(1)-p_(2)=(p_(a)+rhogh)(1)-(p_(a)-rhogh_(2))`
`=rhog(h_(1)+h_(2))`
`=rhog(28 cm)`
`=(3xx10^(3) kg m^(-3))xx(9.8 ms^(-2))(0.28 m)`
`=8.23xx10^(3) Pa ~~8 k Pa`