1.6 किग्रा द्रव्यमान और l लम्बाई की एकसमान लकड़ी की एक डंडी एक चिकनी कड़ी दीवार , जिसकी ऊँचाई `h( lt l)` है , पर आनत तरीके से इस तरह से रखी गई कि डंडी का एक छोटा - सा भाग दीवार से ऊपर निकला हुआ है। डंडी पर दीवार की प्रतिक्रिया बल डंडी के लम्ब रूप में है। डंडी दीवार के साथ `30^@` का कोण बना रही है और डंडी का आधार एक घर्षण वाली जमीन पर है। दीवार से डंडी पर प्रतिक्रिया तथा जमीन से डंडी पर प्रतिक्रिया की मात्रा समान है। `(h)/(l)` का अनुपात एवं डंडी के आधार पर घर्षण बल l है। `(g=10 "मी/से"^2)`.

Options

A. `(h)/(l)=(sqrt(3))/(16),f=(16sqrt(3))/(3)N`
B. `(h)/(l)=(3)/(16),f=(16sqrt(3))/(3)N`
C. `(h)/(l)=(3sqrt(3))/(16),f=(8sqrt(3))/(3)N`.
D. `(h)/(l)=(3sqrt(3))/(16),f=(16sqrt(3))/(3)N`.

Answer

D

Explanation

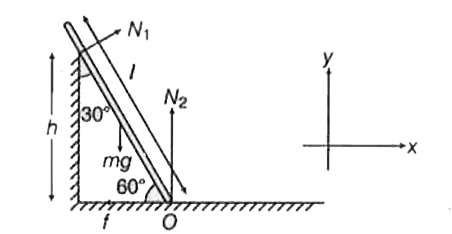
l लम्बाई एवं m द्रव्यमान के एक डण्डे पर लगने वाले बलों पर विचार करें , जोकि चित्रानुसार एक दीवार के सहारे रखा है।
.
क्षैतिज दिशा में बलों के संतुलन से , `Sigma F_(x)=0`
`N_(1) cos 30^@- f=0`
लंबवत दिशा में बलों के संतुलन से , `N_(1) sin 30^@ +N_(2)-mg =0`
निम्नतम बिन्दु O के परितः बलाघूर्ण संतुलन के द्वारा ,`mg (l)/(2) cos 60^@ - N_(1) (h)/(cos 30^@) =0`
दिया है , `N_(1)=N_(2)`
जहा `N_(1)=` चिकनी दीवार के द्वारा डण्डे वाला अभिलम्ब प्रतिक्रिया बल
`N_(2)=` जमीन के द्वारा डण्डे पर लगने वाला घर्षण बल
मान कि ` N_(1)=N_(2)=N`
अतः समी (ii) से , `N_(1) d sin 30^@ +N_(2)=mg`
`rArr (N)/(2) +N=mg`
`N=(2mg)/(3)`.
अतः समी (iii) से, `mg(l)/(2)xx(1)/(2) -N xx (h)/(cos 30^@)=0`
`rArr (mgl)/(4)=(Nh)/(sqrt(3)/(2)) =Nhxx(2)/(sqrt(3))`.
`rArr (mgl)/(4)=(2h)/(sqrt(3))((2mg)/(3))`
`rArr (h)/(l)=(3sqrt(3))/(16)`.
अतः समी (i) के अनुसार डण्डी के आधार पर घर्षण बल , `f=N_(1) cos 30^@`
` =N cos 30^@`
`=(2mg)/(3)xx (sqrt(3))/(2)`
`=(mg)/(sqrt(3))=(1.6xx10)/(sqrt(3))`
`rArr f=(16)/(sqrt(3))N`.