Text Solution
Verified by Experts
Topper's Solved these Questions
LIMITS
CENGAGE ENGLISH|Exercise EXERCISE 2.1|10 VideosLIMITS
CENGAGE ENGLISH|Exercise EXERCISE 2.2|7 VideosLIMITS
CENGAGE ENGLISH|Exercise Comprehension Type|4 VideosJEE 2019
CENGAGE ENGLISH|Exercise Chapter 10|9 VideosLINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORS
CENGAGE ENGLISH|Exercise DPP 1.2|10 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-LIMITS-Solved Examples
- Evaluate lim(ntooo) n^(2){sqrt((1-"cos"(1)/(n))sqrt((1-"cos"(1)/(n))sq...
Text Solution
|
- Evaluate lim(ntooo) {cos((x)/(2))cos((x)/(4))cos((x)/(8))...cos((x)/(2...
Text Solution
|
- Evaluate lim(xto1) "sec" (pi)/(2^(x)).log(e)x.
Text Solution
|
- Evaluate lim(xto0^(+)) (1)/(x)cos^(-1)((sinx)/(x)).
Text Solution
|
- If f(x)=(tanx)/(x), then find lim(xto0)([f(x)]+x^(2))^((1)/({f(x)})), ...
Text Solution
|
- Evaluate lim(ntooo) (1)/(n^(2(log(e)n-log(e)(n+1)))+n).
Text Solution
|
- Evaluate lim(xto0) ((1+x)^(1//x)-e+(1)/(2)es)/(x^(2)).
Text Solution
|
- Evaluate lim(xto0^(+)) x^(m)(logx)^(n),m,n,inN.
Text Solution
|
- If alpha1, ,alpha2, ,alphan are the roots of equation x^n+n a x-b=0, ...
Text Solution
|
- Evaluate lim(xto0) {1^(1//sin^(2)x)+2^(1//sin^(2)x)+...+n^(1//sin^(2)x...
Text Solution
|
- Evaluate lim(xto pi//2) (sinx-(sinx)^(sinx))/(1-sinx+log(e)sinx).
Text Solution
|
- Slove lim(xto0)((1+x)^(1//x)-e)/x
Text Solution
|
- Evaluate lim(ntooo) n^(-n^(2))[(n+2^(0))(n+2^(-1))(n+2^(-2))...(n+2^(-...
Text Solution
|
- ABC is an isosceles triangle inscribed in a circle of radius r. If AB=...
Text Solution
|
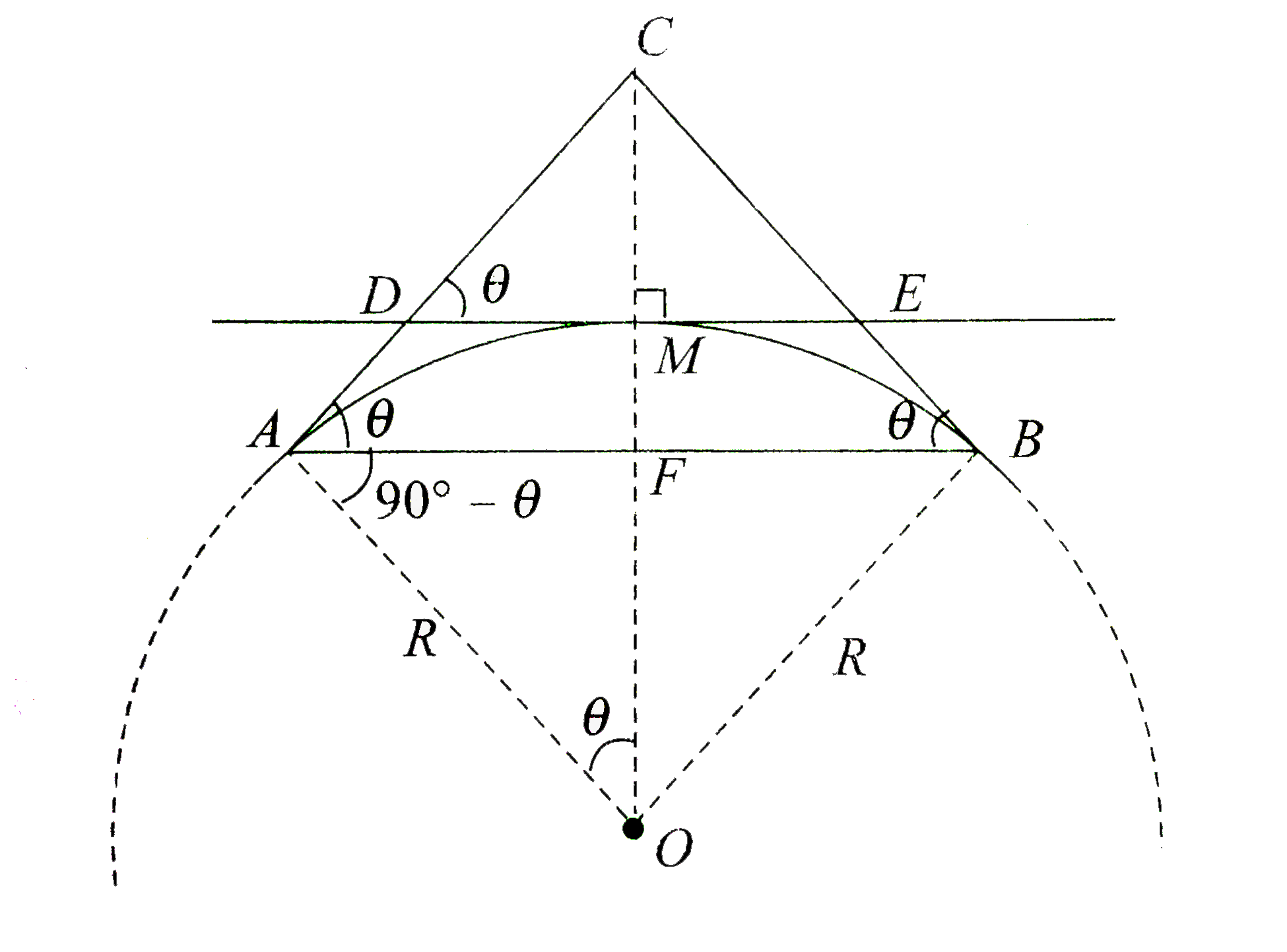
- At the endpoint and midpoint of a circular are AB, tangent lines are ...
Text Solution
|