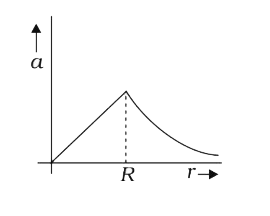
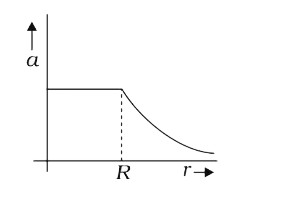
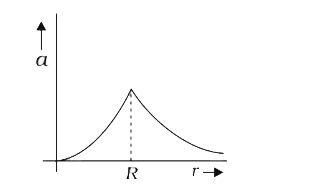
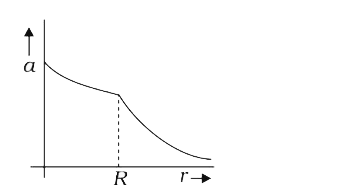
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) SINGLE OPTION CORRECT|14 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE|5 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise Level-2|30 VideosGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE )|111 VideosINTRODUCTION TO VECTORS & FORCES
VMC MODULES ENGLISH|Exercise JEE Advanced ( ARCHIVE LEVEL-2)|12 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-GRAVITATION-JEE Main (Archive)
- The dependence of acceleration due to gravity g on the distance r from...
Text Solution
|
- If the earth has no rotational motion, the weight of a person on the e...
Text Solution
|
- The mass density of a spherical body is given by rho(r)=k/r for r le R...
Text Solution
|
- Suppose that angular velocity of rotation of earth is increased. Then...
Text Solution
|
- The relative uncertainty in the period of a satellite orbiting around ...
Text Solution
|
- A body of mass m is moving in a circular orbit of radius R about a pla...
Text Solution
|
- Take the mean distance of the moon and the sun from the earth to be0.4...
Text Solution
|
- Four identical particles of mass M are located at the corners of a squ...
Text Solution
|
- A rocket has to be launched from earh in such a way that it never retu...
Text Solution
|
- A solid sphere of radius a and mass m is surrounded by cocentric spher...
Text Solution
|
- A test particle is moving in a circular orbit in the gravitational fie...
Text Solution
|
- A ball is thrown upward with an initial velocity V0 from the surface o...
Text Solution
|
- If g is acceleration due to gravity on the surface of the earth, havin...
Text Solution
|
- A spaceship orbits around a planet at a height of 20 km from its surfa...
Text Solution
|
- The ratio of the weight of a body on the Earth’s surface to that on th...
Text Solution
|
- The energy required to take a satellite to a height ‘h’ above Earth su...
Text Solution
|
- If the angular momentum of a planet of mass m, moving around the Sun i...
Text Solution
|
- Two stars of masses 3 xx 10^(31) kg each, and at distance 2 xx 10^(11)...
Text Solution
|
- A satellite is moving with a constant speed v in circular orbit around...
Text Solution
|
- A satellite is revolving in a circular orbit at a height h from the ea...
Text Solution
|