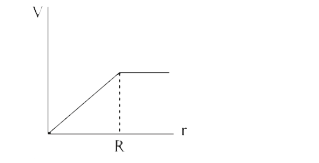
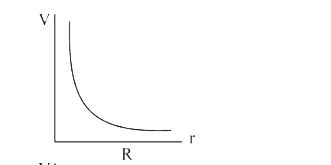
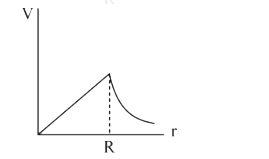
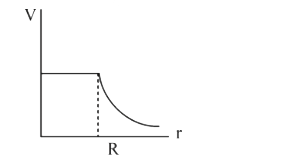
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
GRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive) MULTIPLE OPTIONS CORRECT TYPE|5 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Advance (Archive)ASSERTIOIN AND REASON|1 VideosGRAVITATION
VMC MODULES ENGLISH|Exercise JEE Main (Archive)|43 VideosGASEOUS STATE & THERMODYNAMICS
VMC MODULES ENGLISH|Exercise JEE ADVANCED (ARCHIVE )|111 VideosINTRODUCTION TO VECTORS & FORCES
VMC MODULES ENGLISH|Exercise JEE Advanced ( ARCHIVE LEVEL-2)|12 Videos
Similar Questions
Explore conceptually related problems
VMC MODULES ENGLISH-GRAVITATION-JEE Advance (Archive) SINGLE OPTION CORRECT
- If the radius of the earth were to shrink by one per cent, its mass re...
Text Solution
|
- If g be the acceleration due to gravity of the earth's surface, the ga...
Text Solution
|
- Imagine a light planet revolving around a very massive star in a circu...
Text Solution
|
- If the distance between the earth and the sun were half its present va...
Text Solution
|
- A satellite S is moving in an elliptical orbit around the earth. The m...
Text Solution
|
- A simple pendulum has a time period T(1) when on the earth's surface a...
Text Solution
|
- A geo-stationary satellite orbits around the earth in a circular orbit...
Text Solution
|
- A binary star system consists of two stars A and B which have time per...
Text Solution
|
- A spherically symmetric gravitational system of particles has a mass d...
Text Solution
|
- A thin uniform disc (see figure) of mass M has outer radius 4R and in...
Text Solution
|
- A satellite is moving with a constant speed v in circular orbit around...
Text Solution
|
- A planet of radius R=(1)/(10)xx(radius of Earth) has the same mass den...
Text Solution
|
- A rocket is launched normal to the surface of the earth, away from the...
Text Solution
|
- Consider a spherical gaseous cloud of mass density rho(r) in a free sp...
Text Solution
|