Home
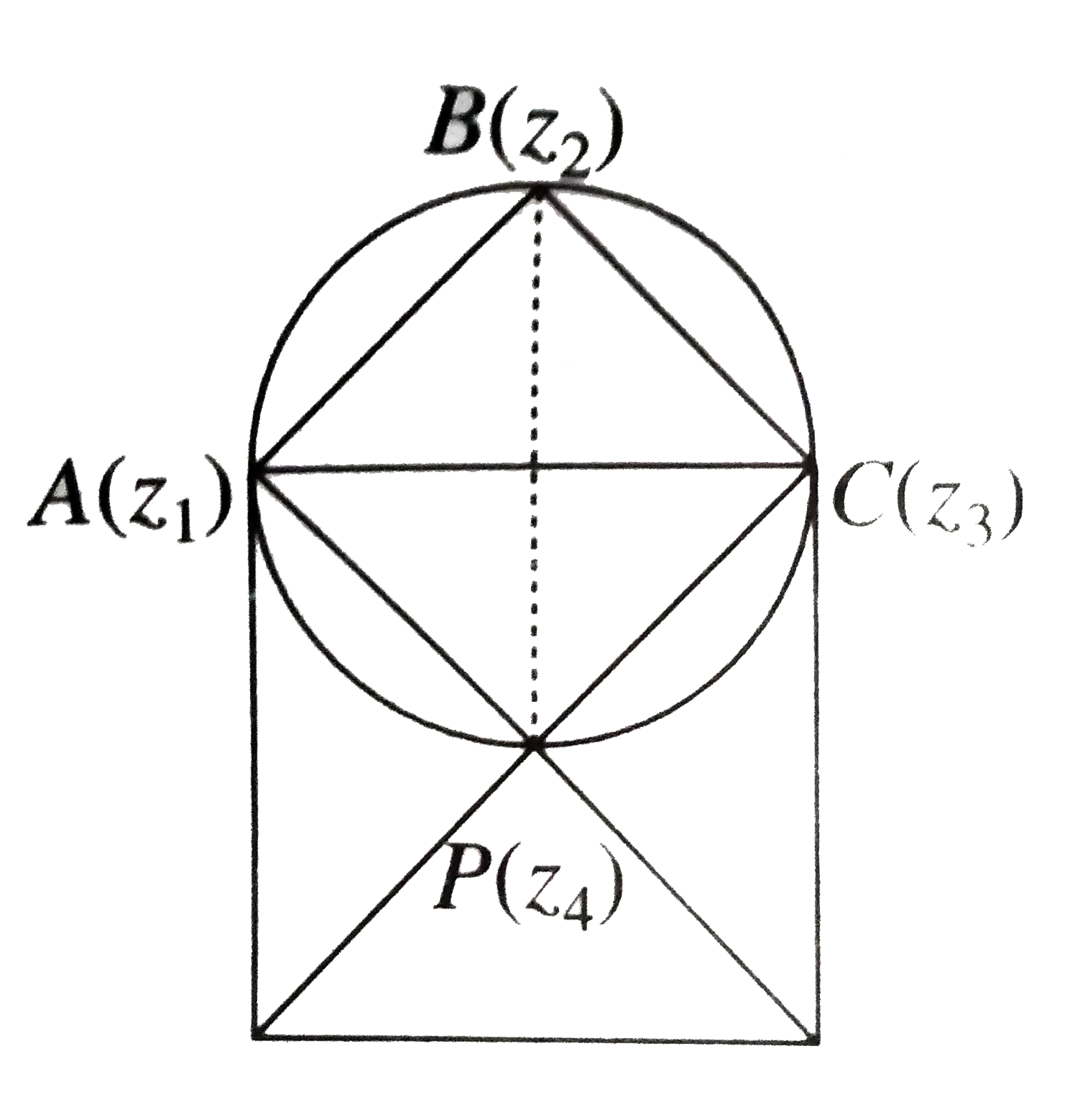
Class 12
MATHS
Let z(1), z(2), z(3) are the vertices of...

Let `z_(1)`, `z_(2)`, `z_(3)` are the vertices of `DeltaABC`, respectively, such that `(z_(3)-z_(2))/(z_(1)-z_(2))` is purely imaginery number. A square on side `AC` is drawn outwardly. `P(z_(4))` is the centre of square, then

A

`|z_(1)-z_(2)|=|z_(2)-z_(4)|`

B

`arg((z_(1)-z_(2))/(z_(4)-z_(2)))+arg((z_(3)-z_(2))/(z_(4)-z_(2)))=+(pi)/(2)`

C

`arg((z_(1)-z_(2))/(z_(4)-z_(2)))+arg((z_(3)-z_(2))/(z_(4)-z_(2)))=0`

D

`z_(1)`, `z_(2)`, `z_(3)` and `z_(4)` lie on a circle

Text Solution

Verified by Experts

The correct Answer is:
C, D
`(c,d)` `P` is centre of square `implies AP=PC` and `/_APC=(pi)/(2)`
`/_ABC` is also `(pi)/(2)`.
`implies ABCP` is cyclic quadrilateral
`impliesA,B,C,P` lie on a circle.
`implies` In circl chord, `AP=PC`
`implies` arc `AP=` are `PC`
`implies/_ABP=/_PBC`
`implies BP` is angular bisector.
Let `arg((z_(1)-z_(2))/(z_(4)-z_(2)))=-alpha`........`(i)`
`impliesarg((z_(3)-z_(2))/(z_(4)-z_(2)))=alpha`..........`(ii)`
Add `(i)` and `(ii)`, `arg((z_(1)+z_(2))/(z_(4)-z_(2)))+arg((z_(3)-z_(2))/(z_(4)-z_(2)))=0`
Promotional Banner

Topper's Solved these Questions

  • COMPLEX NUMBERS

    CENGAGE PUBLICATION|Exercise Matching Column|1 Videos

  • COMPLEX NUMBERS

    CENGAGE PUBLICATION|Exercise Comprehension|11 Videos

  • COMPLEX NUMBERS

    CENGAGE PUBLICATION|Exercise MULTIPLE CORRECT ANSWER TYPE|6 Videos

  • CIRCLES

    CENGAGE PUBLICATION|Exercise Comprehension Type|8 Videos

  • CONIC SECTIONS

    CENGAGE PUBLICATION|Exercise All Questions|102 Videos

Similar Questions

Explore conceptually related problems

If A(z_1), B(z_2), C(z_3) are the vertices of an equilateral triangle ABC, then arg((z_2+z_3-2z_1)/(z_3-z_2)) is equal to

If A(z_1),B(z_2),C(z_3) and D(z_4) be the vertices of the square ABCD then

If z_1, z_2 are complex number such that (2z_1)/(3z_2) is purely imaginary number, then find |(z_1-z_2)/(z_1+z_2)| .

If A(z_(1)) , B(z_(2)) , C(z_(3)) are vertices of a triangle such that z_(3)=(z_(2)-iz_(1))/(1-i) and |z_(1)|=3 , |z_(2)|=4 and |z_(2)+iz_(1)|=|z_(1)|+|z_(2)| , then area of triangle ABC is

z_(1) and z_(2)( ne z_(1)) are two complex numbers such that |z_(1)|=|z_(2)| . Sho that the real part of (z_(1)+z_(2))/(z_(1)-z_(2)) is zero.

Let A(z_(1)) and B(z_(2)) are two distinct non-real complex numbers in the argand plane such that (z_(1))/(z_(2))+(barz_(1))/(z_(2))=2 . The value of |/_ABO| is

If the complex numbers z_(1),z_(2),z_(3) represents the vertices of an equilaterla triangle such that |z_(1)|=|z_(2)|=|z_(3)| , show that z_(1)+z_(2)+z_(3)=0

Let z_(1) and z_(2) be any two non-zero complex numbers such that 3|z_(1)|=2|z_(2)|. "If "z=(3z_(1))/(2z_(2)) + (2z_(2))/(3z_(1)) , then

If z_1, z_2 and z_3 , are the vertices of an equilateral triangle ABC such that |z_1 -i| = |z_2 -i| = |z_3 -i| .then |z_1 +z_2+ z_3| equals:

If z_(1)and z_(2) be any two non-zero complex numbers such that |z_(1)+z_(2)|=|z_(1)|+|z_(2)| then prove that, arg z_(1)=arg z_(2) .