Text Solution
Verified by Experts
Topper's Solved these Questions
MATRICES
CENGAGE ENGLISH|Exercise CAE 13.1|5 VideosMATRICES
CENGAGE ENGLISH|Exercise CAE 13.2|6 VideosMATRICES
CENGAGE ENGLISH|Exercise Single correct Answer|34 VideosMATHMETICAL REASONING
CENGAGE ENGLISH|Exercise Archives|10 VideosMETHODS OF DIFFERENTIATION
CENGAGE ENGLISH|Exercise Single Correct Answer Type|46 Videos
Similar Questions
Explore conceptually related problems
CENGAGE ENGLISH-MATRICES-ILLUSTRATION
- Given a matrix A=[a b c b c a c a b],w h e r ea ,b ,c are real positiv...
Text Solution
|
- If M is a 3xx3 matrix, where det M=1a n dM M^T=1,w h e r eI is an iden...
Text Solution
|
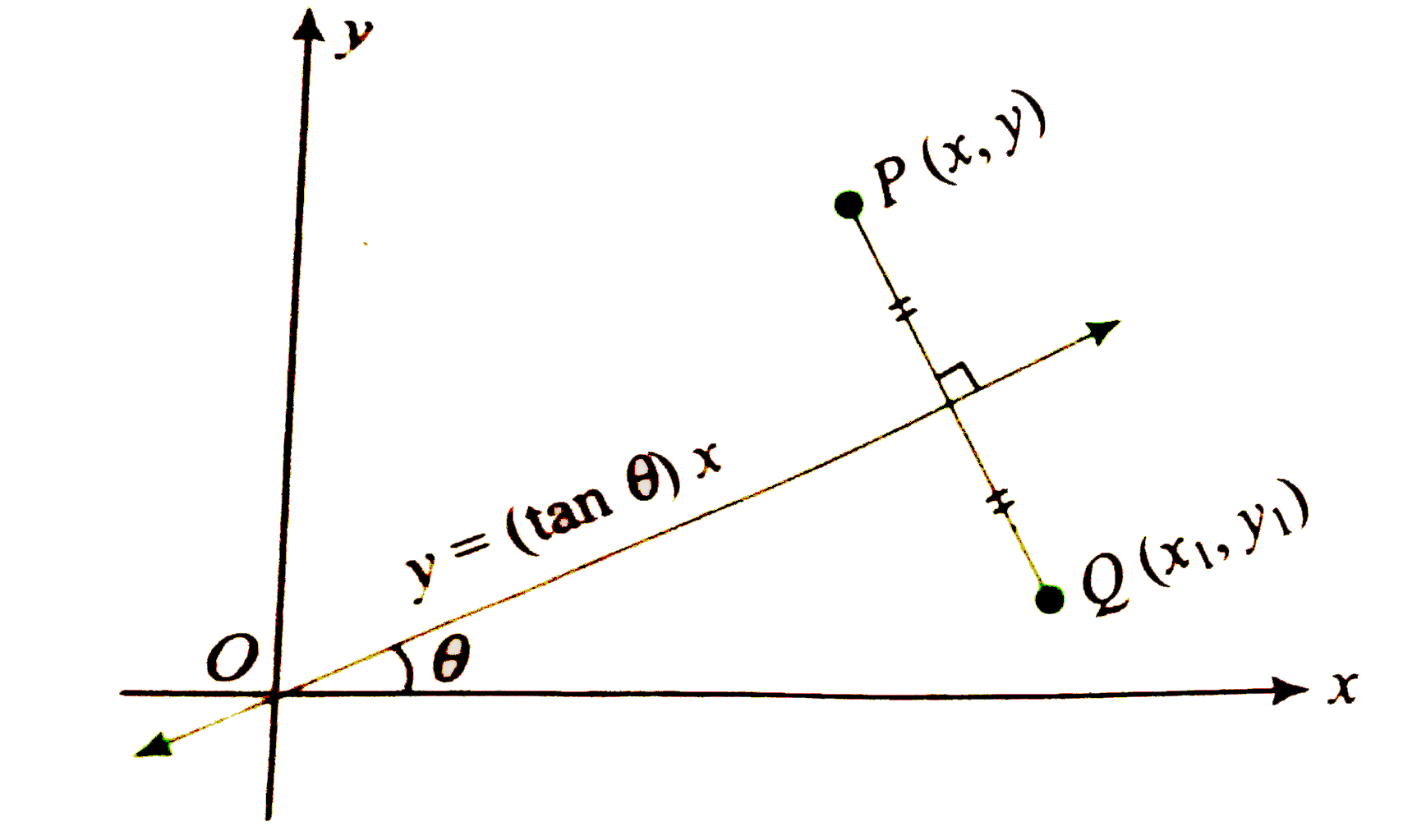
- Consider point P(x, y) in first quadrant. Its reflection about x-axis ...
Text Solution
|
- If A=[[2,-2,-4],[-1,3,4],[1,-2,-3]] then A is 1) an idempotent matrix ...
Text Solution
|
- If A= [(1,1,3),(5,2,6),(-2,-1,-3)] then find A^(14)+3A-2I
Text Solution
|
- The matrix A=[-5-8 0 3 5 0 1 2-] is a. idempotent matrix b. involut...
Text Solution
|
- If abc=p and A=[(a,b,c),(c,a,b),(b,c,a)], prove that A is orthogonal i...
Text Solution
|
- Let A be an orthogonal matrix, and B is a matrix such that AB=BA, then...
Text Solution
|
- Find the adjoint of the matrix A=[(1,1,1),(2,1,-3),(-1,2,3)].
Text Solution
|
- If S=[((sqrt(3)-1)/(2sqrt(2)),(sqrt(3)+1)/(2sqrt(2))),(-((sqrt(3)+1)/(...
Text Solution
|
- If A is a square matrix such that A(adjA)=[(4,0,0),(0,4,0),(0,0,4)], t...
Text Solution
|
- Let A be a square matrix of order 3 such that adj. (adj. (adj. A)) =...
Text Solution
|
- Let A =[(1,-1,1),(2,1,-3),(1,1,1)] and 10B=[(4,2,2),(-5,0,alpha),(...
Text Solution
|
- Matrices a and B satisfy AB=B^(-1), where B=[(2,-1),(2,0)]. Find (i...
Text Solution
|
- Given the matrices A and B as A=[(1,-1),(4,-1)] and B=[(1,-1),(2,-2)]....
Text Solution
|
- If M is the matrix [(1,-3),(-1,1)] then find matrix sum(r=0)^(oo) ((-1...
Text Solution
|
- Let p be a non singular matrix, and I + P + p^2 + ... + p^n = 0, then ...
Text Solution
|
- If A and B are square matrices of same order such that AB=O and B ne O...
Text Solution
|
- If A is a symmetric matrix, B is a skew-symmetric matrix, A+B is nonsi...
Text Solution
|
- If the matrices, A, B and (A+B) are non-singular, then prove that [A(A...
Text Solution
|